ДАНО
Y = 4*(x²+2x+1)/(x² +2x+ 4)
ИССЛЕДОВАНИЕ
1.Область определения D(x) - непрерывная Х∈(-∞;+∞).
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y=0 при х = -1.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.
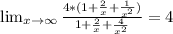
limY(+∞) = 4.
Горизонтальная асимптота - Y = 4.
5. Исследование на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни чётная ни нечётная.
6. Производная функции.
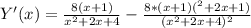
Корень при Х=-1.
Схема знаков производной.
(-∞)__(<0-убыв)__(х= -1)_(<0-убыв)__(+∞)
7. Локальные экстремумы.
Максимума - нет, минимум – Ymin(-1) = 0.
8. Интервалы монотонности.
Убывает - Х∈(-∞;-1]. Возрастает - Х∈[-1;+∞)
9. Вторая производная - Y"(x).
Корни производной - точки перегиба: х1 =-2, х2= 0.
9. Выпуклая “горка» Х∈(-∞;-2)∪(0;+∞),
Вогнутая – «ложка» Х∈(-2;0).
10. Область значений Е(у) У∈[0;4)
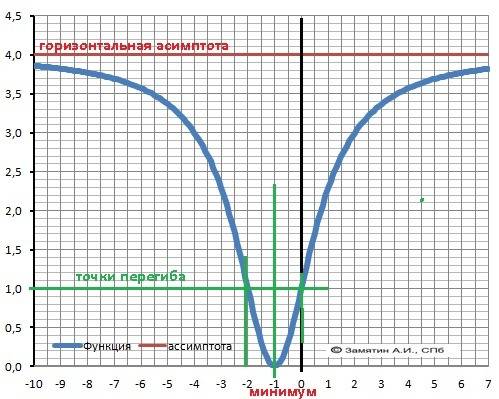
11. График в приложении
ответ: 60
Пошаговое объяснение:
Варианты задуманного двузначного числа: 15, 30, 45, 60, 75, 90.
Сначала проверяем нечетные числа:
Добавляем последнюю цифру данного числа - 15 -> 155
По теории деления на 3, 6, 9, сложим все цифры числа 155, чтобы узнать, делится ли сумма на 3.
155:
1 + 5 + 5 = 11, число 11 не делится на 3, а значит не делится на 9.
Можно пропустить нечетные числа.
Рассмотрим четные числа:
Аналогично осмотру нечетных чисел, т.е. так же проверяем четные.
300:
3 + 0 + 0 = 3, число 3 делится на 3, но не одновременно на 9.
300/9 = 33 3/9 (3 - остаток, как мы знаем, а 9 - число, на которое мы делим)
Нам по заданий нужно найти число, которое даёт остаток 6 при делении на 9.
600:
6 + 0 + 0 = 6, число 6 делится на 3, но опять же вместе с этим не делится на 9.
600/9 = 66 6/9 (6 - остаток, 9 - делитель)
900:
9 + 0 + 0 = 9, число делится на 3, и теперь уже заодно на 9.
Мы нашли нужное для ответа задуманное двузначное число по условиям задачи: 60.
3(х+24)+4х=478
3х+72+4х=478
7х=406
х=58 центов стоит пачка творога.
ответ: 58 центов.