73 и 37
Пошаговое объяснение:
Пусть ab искомое двузначное число, где a и b цифры. По условию
1) a+b=21, a·b=10 или 2) a+b=10, a·b=21, других вариантов нет!
Так как a и b цифры, то есть a<10 и b<10, то a+b<10+10=20<21. Поэтому в случае 1) нет решения.
Решаем систему 2):
\begin{gathered}\displaystyle \left \{ {{a+b=10} \atop {a*b=21}} \right. left \{ {{a=10-b} \atop {(10-b)*b=21}} \right.\end{gathered}
{
a∗b=21
a+b=10
{
(10−b)∗b=21
a=10−b
b²-10·b+21=0
D=10²-4·1·21=100-84=16=4²
b₁=(10-4)/2=6/2=3, b₂=(10+4)/2=14/2=7.
Тогда
a₁=10-b₁=10-3=7, a₂=10-b₂=10-7=3.
Получим числа
73 и 37.
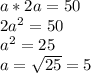Это в том случае, если оба числа положительные, тогда меньшее равно 5, большее 5*2=10, а их произведение 5*10=50. Однако, если числа отрицательные, то получается следующая картина: Рассмотрим отрицательные числа. Пусть теперь b-наибольшее число из двух, следовательно наименьшее будет 2*b. Их произведение равно 50. Решим уравнение : 
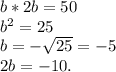Такие образом, получаем два ответа: когда числа положительные и когда отрицательные. В первом случае (пол.) наим. число 5, когда же числа отр. наименьшее число -10.
