(6х+4)/7 + (9-5х)/6 = (х-2)
Приводим обе части уравнения к общему знаменателю 42
(6х + 4) · 6 + (9 - 5х) · 7 = (х - 2) · 6 · 7
36х + 24 + 63 - 35х = 42х - 84
36х - 35х - 42х = -84 - 24 - 63
-41х = -171
х = -171 : (-41)
х = 171/41
х = 4 целых 7/41
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Проверка: (6 · 171/41 + 4)/7 + (9 - 5 · 171/41)/6 = 4 7/41 - 2
(1026/41 + 4)/7 + (9 - 855/41)/6 = 2 7/41
29 1/41 : 7 - 11 35/41 : 6 = 2 7/41
1190/287 - 486/246 = 2 7/41
4 6/41 - 1 40/41 = 2 7/41
3 47/41 - 1 40/41 = 2 7/41
2 7/41 = 2 7/41 - верно
ответ: при х = 4 целых 7/41 выражения будут равны.
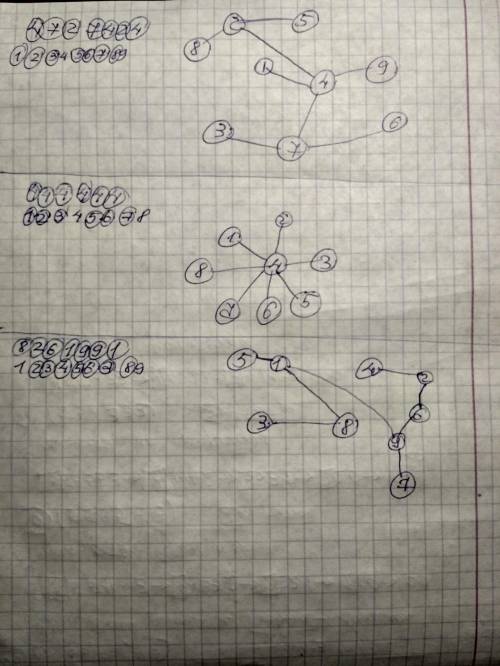
Задание 1
ответ в приложении
Задание 2
Тут, очевидно, опечатка, k<n. В дереве на n вершинах не может быть вершины степени n.
n=1:
k=0 - одно дерево, состоящее из одной вершины.n=2:
k=0 => граф не связный => не деревоk=1 => одно дерево, состоящее из одного ребраn>2:
k=0 => граф не связный => не деревоk>0 => Тогда каждому дереву поставим в соответствие код Прюфера. Его длина - n-2. Т.к. вершина 1 имеет степень k, то встречается в нем k-1 раз. Тогда для остальных n-1 вершин остается n-2-(k-1)=n-k-1 мест. Тогда всего таких кодов Прюфера, и, следовательно, деревьев,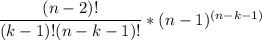
Задание 3
Найти количество деревьев с n вершинами, имеющими вершину степени n-2.
Зафиксируем номер этой вершины. Тогда в коде Прюфера она встречается n-3 раз. Тогда для остальных n-1 вершин остается n-2-(n-3)=1 место. Кол-во выбора номера вершины степени n-2 из n равно n. Тогда искомое число деревьев равно 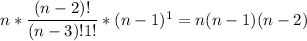
в:а=4:3
4а=3в