1)
1)-(x-1)(8x²+4x)=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=02)
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=02)(-0,3+4)(4x-0,3)=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=02)(-0,3+4)(4x-0,3)=0-1,2x+0,09+16x-1,2=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=02)(-0,3+4)(4x-0,3)=0-1,2x+0,09+16x-1,2=014,8x-1,11=0
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=02)(-0,3+4)(4x-0,3)=0-1,2x+0,09+16x-1,2=014,8x-1,11=014,8x=1,11
1)-(x-1)(8x²+4x)=0(-x+1)(8x²+4x)=0-8x³-4x²+8x²+4x=0-8x³+4x²+4x=0-4x(2x²-1)+4x=02x²-1=02x²=1x=+_корень2/2-4x+4x=0-x=02)(-0,3+4)(4x-0,3)=0-1,2x+0,09+16x-1,2=014,8x-1,11=014,8x=1,11×=0,075
Розглянемо випадкову величину 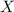 — число білих кульок серед вилучених.
— число білих кульок серед вилучених.
Всього можливих подій: 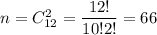 .
.
1) Імовірність того, що серед навмання вилучених 2 кульок не буде білої :
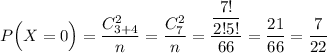
2) Імовірність того, що серед навмання вилучених 2 кульок буде одна біла кулька:
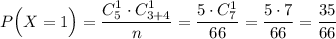
3) Імовірність того, що серед навмання вилучених 2 кульок всі кульки будуть білими:
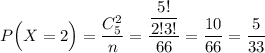
Закон розподілу випадкової величини 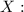
Xi 0 1 2
Pi 7/22 35/66 5/33
Знайдемо математичне сподівання випадкової величини 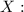
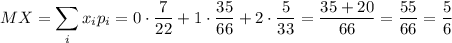
Дисперсія випадкової величини 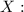
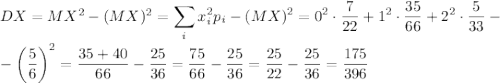
Середнє квадратичне відхилення:
б)