ответ: 50/3 см.
Пошаговое объяснение:
Пусть a - сторона отрезаемого квадрата, тогда объём коробки V(a)=a*(100-2*a)²=4*a³-400*a²+10000*a см³. Задача сводится к нахождению максимума функции V(a) и нахождения соответствующего a. Находим производную V'(a)=12*a²-800*a+10000. Приравнивая её к нулю и сокращая на 4, приходим к квадратному уравнению 3*a²-200*a+2500=0. Оно имеет решения a1=50 см и a2=50/3 см. Если a<50/3, то V'(a)>0; если 50/3<a<50, то V'(a)<0; если a>50, то V'(a)>a. Отсюда следует, что функция V(a) имеет максимум при a=50/3 и минимум при a=50. Значит, сторона выбрасываемого квадрата должна быть равна 50/3 см.
Пошаговое объяснение:
Дано трехзначное число abc, где а- число сотен , b- число десятков , с - число единиц. При этом b=c. Получаем уравнение
a+b+b=12
a+2b=12
Если в числе(100a+10b+b ( c=b) поменять местами первую и вторую цифры , получим число 100b+10a+b . Составим уравнение
(100b+10a+b)-(100a+10b+b)= 270
101b+10a-100a-11b=270
90b-90a=270
разделим на 90
b-a=3
Получаем систему уравнений :
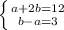
из второго уравнения
b=3+a
подставим в первое уравнение
а+2(3+а)=12
а+6+2а=12
3а=6
а=2
b=3+2=5
Искомое число 255
Проверка :
2+5+5=12
525-255= 270
270=270
Осталось 4 замка и 4 ключа. С трех (или меньше) попыток определяем второй замок. Если к трем замкам не подходит, то четвертый не проверяем. Ключ подойдет.
Осталось 3 замка и 3 ключа. С двух попыток определяем третий замок.
Осталось 2 замка и 2 ключа. Берем любой ключ. Он либо подходит к одному из замков, тогда второй ключ подходит ко второму замку, либо не подходит, тогда это ключ от второго замка, а другой ключ - от превого. Это решаем одной попыткой.
Всего максимальное количество попыток 4+3+2+1= 10
Так что, барон прав.