Периметр прямоугольника по формуле: Р = 2*(a+b).
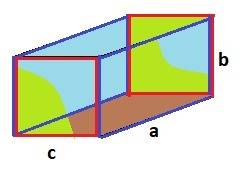
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2
Периметр прямоугольника по формуле: Р = 2*(a+b).
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2

y^2+2(a-2)*y+a^2-1>0
(y+(a-2))^2>1-a^2-a^2+4a-4
(y+(a-2))^2>4a-3
если а<3/4 неравенство верно для всех х.
Кроме того: х меньше либо равно 3 и больше либо равно 1. Значит выражение в скобках меньше либо равно а+1 и больше либо равно а-1
(a-1)^2>4a-3 a>3+sqrt(5) или a<3-sqrt(5), но 3-sqrt(5)>3/4
ответ:а<3-sqrt(5) или a>3+sqrt(5)