Математика: Построить б5/3 и м5/3 от нот до диез си бимоль фа и ля !

Построить б5/3 и м5/3 от нот до диез си бимоль фа и ля !

👇

Ответ:

jamikzara

10.12.2022

М53: м3+б3, Б53: б3+м3. Расставляем интервалы всегда снизу вверх.
М53: фа - ля бемоль - до; Б53: до бемоль - ми бемоль - соль бемоль; М53: соль бемоль - си дубль бемоль (два бемоля рядом) - ре бемоль; Б53: ре - фа диез - ля; М53: фа бемоль - ля дубль бемоль - до бемоль; Б53: си - ре диез - фа диез; М53: ми - соль - си.

4,8(1 оценок)

Открыть все ответы

Ответ:

dangoreh

10.12.2022

$X=\left[\begin{array}{ccc}\frac{-6}{11}&\frac{-21}{22}\\\frac{9}{22}&\frac{12}{11}\end{array}\right]$

Пошаговое объяснение:

Для уравнения

3·C·(A·X+3·B)=0

сначала проверим существование обратной к C матрицы C⁻¹. Для этого достаточно вычислить определитель матрицы С:

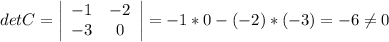
$detC=\left|\begin{array}{ccc}-1&-2\\-3&0\end{array}\right| = -1*0-(-2)*(-3)=-6\neq 0$

Отсюда следует, что обратная к C матрицы C⁻¹ существует. Тогда

3·C·(A·X+3·B)=0 ⇔ A·X+3·B=(3·С)⁻¹·0 ⇔ A·X+3·B=0 или A·X = -3·B.

Находим обратной к А матрицу А⁻¹. Для этого сначала вычислим определитель матрицы А:

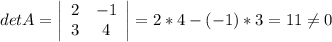
$detA=\left|\begin{array}{ccc}2&-1\\3&4\end{array}\right| = 2*4-(-1)*3=11\neq 0$

Транспонируем матрицу А:

$A^{T}=\left[\begin{array}{ccc}2&4\\3&-1\end{array}\right]$

Находим алгебраические дополнение к элементам транспонированной матрицы 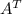$A^{T}$ :

алгебраическое дополнение элемента 2 - это 4;

алгебраическое дополнение элемента 3 - это -(-1)=1;

алгебраическое дополнение элемента -1 - это -3;

алгебраическое дополнение элемента 4 - это 2.

Тогда обратная к А матрицу А⁻¹ имеет вид:

$A^{-1}=\frac{1}{11} \left[\begin{array}{ccc}4&1\\-3&2\end{array}\right]= \left[\begin{array}{ccc}\frac{4}{11}&\frac{1}{11}\\\frac{-3}{11}&\frac{2}{11}\end{array}\right]$

Вычислим матрицу -3·B:

$-3*B=\left[\begin{array}{ccc}\frac{-3}{2} &-3 \\0&\frac{3}{2} \end{array}\right]$

Решением матричного уравнения будет

X=А⁻¹·(-3·B)

то есть

$X=\left[\begin{array}{ccc}\frac{4}{11}&\frac{1}{11}\\\frac{-3}{11}&\frac{2}{11}\end{array}\right]*\left[\begin{array}{ccc}\frac{-3}{2} &-3 \\0&\frac{3}{2} \end{array}\right]=$

$=\left[\begin{array}{ccc}\frac{4}{11}*\frac{-3}{2}+\frac{1}{11}*0&\frac{4}{11}*(-3)+\frac{1}{11}*\frac{3}{2}\\\frac{-3}{11}*\frac{-3}{2}+\frac{2}{11}*0&\frac{-3}{11}*(-3)+\frac{2}{11}*\frac{3}{2}\end{array}\right]=$