1) 48 = 2*2*2*2*3 и 84=2*2*3*7 и НОД(48,84)= 2*2*3 = 12
2) 70=2*5*7 и 98=2*7*7 и НОД(70,98)=2*7=14
3) 16 = 2*2*2*2 и 45=3*3*5 и НОД(16,45)=1- делителей нет.
4) 52= 2*2*13 и 78= 2*3*13 и НОД(52,78)=2*13 = 26
5) 44= 2*2*11 и 65=5*13 и НОД(44,65)=1 - делителей нет
6) 72=2*2*2*3*3 и 96=2*2*2*2*2*3 и НОД(72,96)=2*2*2*3 = 24
7) 78=2*3*13 и 117=3*3*13 и 195=3*5*13 и НОД(78,117,195)=39
8) 110=2*5*11 и 154=2*7*11 и 286=2*11*13 и НОД(110,154,286)=22
9) 90=2*3*3*5 и 126=2*3*3*7 и 162=2*3*3*3*3 и НОД(90,126,162)=18.
Подробнее - на -
Чтобы решить данную задачу, введем условную переменную "Х", через которую обозначим первоначальное число.
Действие первое: определим, каким будет число после его уменьшения на 30%.
В результате получаем Х - (30% х Х) / 100% = 0,7Х.
Вторым действием определим, каким будет число после его увеличения на 30%.
В результате получаем 0,7Х + (30% х 0,7Х) / 100% = 0,91Х.
Теперь определим, на сколько процентов уменьшилось конечное число по сравнению с первоначальным числом.
В результате получаем ((Х - 0,91Х) / Х) х 100% = 9%.
ответ: первоначальное число уменьшится на 9%.
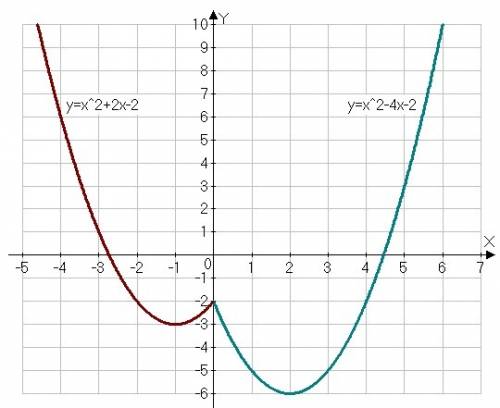
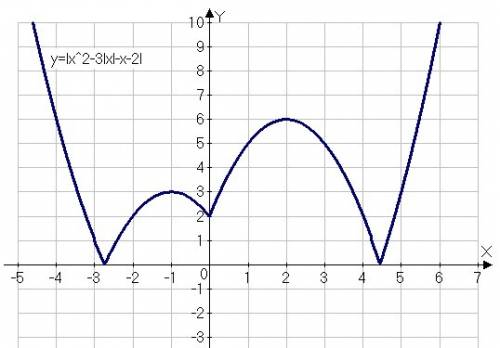
Это значит, что вершины парабол становявтся
А'(2;6) и В'(-1;3)