https://www.kontrolnaya-rabota.ru/s/equal-one/any-uravnenie/?ef-TOTAL_FORMS=20&ef-INITIAL_FORMS=0&ef-MIN_NUM_FORMS=0&ef-MAX_NUM_FORMS=1000&X=x&solve=%283-4%D1%85%29%5E2%283%D1%85%2B2%29%3C0&ef-0-s=&ef-1-s=&ef-2-s=&ef-3-s=&ef-4-s=&ef-5-s=&ef-6-s=&ef-7-s=&ef-8-s=&ef-9-s=&ef-10-s=&ef-11-s=&ef-12-s=&ef-13-s=&ef-14-s=&ef-15-s=&ef-16-s=&ef-17-s=&ef-18-s=&ef-19-s=&a0=-10&b0=%2B10
Пошаговое объяснение:
На этой ссылке ты можешь всё найти ( вроде он безопасный)
Прямую называют асимптотой графика функции, если расстояние между этой прямой и точкой графика стремится к нулю при отдалении этой точки от начала координат.
Асимптоты бывают вертикальными, горизонтальными и наклонными.
Если существует такое число  , что
, что 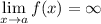 , то
, то  — вертикальная асимптота графика функции
— вертикальная асимптота графика функции 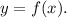
Если имеем функцию 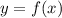 , для которой существуют
, для которой существуют 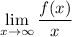 и
и 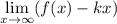 , причем
, причем 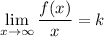 и
и 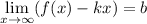 , то прямая
, то прямая 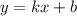 при
при 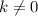 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 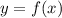 , а при
, а при 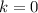 — горизонтальной асимптотой, уравнение которой
— горизонтальной асимптотой, уравнение которой 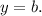
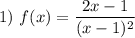
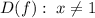
Поскольку в точке 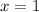 функция имеет разрыв, то прямая
функция имеет разрыв, то прямая 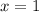 может оказаться вертикальной асимптотой. Имеем:
может оказаться вертикальной асимптотой. Имеем:
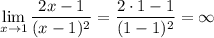
Следовательно, 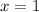 — вертикальная асимптота.
— вертикальная асимптота.
Имеем далее:
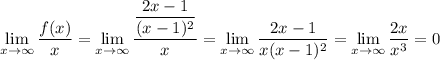
Поскольку 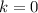 , то если асимптота существует, то она будет горизонтальной асимптотой.
, то если асимптота существует, то она будет горизонтальной асимптотой.
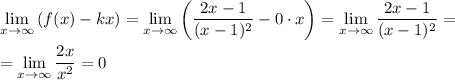
Итак, имеем уравнение горизонтальной асимптоты: 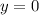
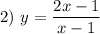
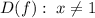
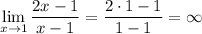
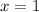 — вертикальная асимптота.
— вертикальная асимптота.
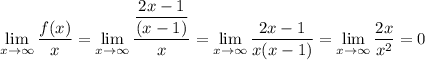
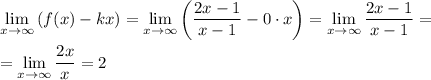
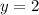 — горизонтальная асимптота.
— горизонтальная асимптота.
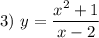
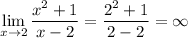
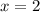 — вертикальная асимптота.
— вертикальная асимптота.
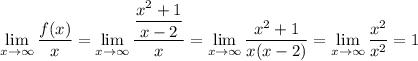
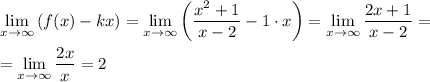
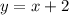 — наклонная асимптота.
— наклонная асимптота.
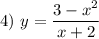
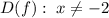
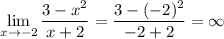
 — вертикальная асимптота.
— вертикальная асимптота.
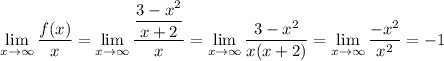
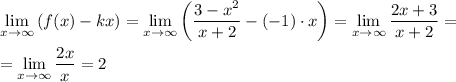
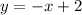 — наклонная асимптота.
— наклонная асимптота.
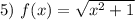
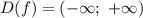
Нет вертикальных асимптот.
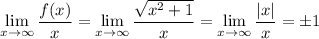
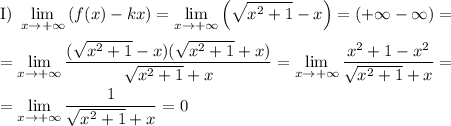
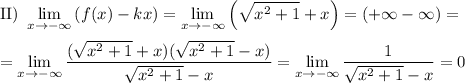
 и
и 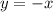 — наклонные асимптоты.
— наклонные асимптоты.
(31200-8320):2=11400(кг) — собрано инжира
31200-11440=19760(кг) — собрано фиников
ответ: 11400 кг, 19760 кг.