ответ: будет.
Пошаговое объяснение:
Если функция дифференцируема в некоторой точке x=x0, то она и непрерывна в ней. Действительно, пусть функция y(x) дифференцируема в точке x=x0. Это значит, что lim Δy/Δx=y'(x0) при Δx⇒0. Отсюда Δy/Δx=y'(x0)+α(x), где α(x) - бесконечно малая величина при x⇒x0, т.е. при Δx⇒0. Тогда Δy=y'(x0)*Δx+α(x)*Δx, а так как y'(x0) - конечное число, то при Δx⇒0 и Δy⇒0. А это и означает, что в точке x=x0 функция непрерывна. Подставляя теперь x0=2, приходим к утвердительному ответу.
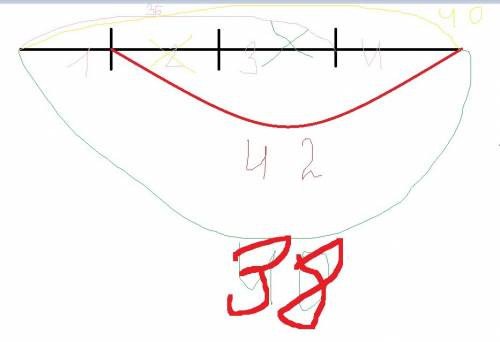
Четыре неизвестных - a,b,c,d - пишем четыре понятных уравнения.
1) b+c+d = 42
2) a+c+d = 40
3) a+b+d = 38
4) a+b+c = 36
На вид много и сложно?! - сложим все четыре уравнения.
5) 3*(a+b+c+d) = 42+40+38+36 = 156
Разделили на 3 и получили
6) a+b+c+d+ =156:3 = 52 - всего открыток.
А теперь вычитаем из ур. 6) уравнения 1...4.
7) a = 52 - 42 = 10
8) b = 52 -40 = 12
9) c = 52 - 38 = 14
10) d = 52 - 36 = 16
ОТВЕТ: У девочек 10,12,14 и 16 шт.