1. б) (-3; 8]
2. а)
3. x∈ [-1; 2)
4. x∈ (-3; +∞)
5. x∈ (-1,5; 6]
6. x∈ [1/5; 2]
7. x∈ (-∞; 12]
8. x∈ [-2; 3]
Пошаговое объяснение:
1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3. 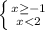
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4. 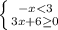

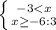
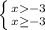
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
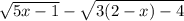
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:

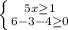


1/5 ≤ x ≤ 2 или x∈ [1/5; 2]
7. Решите совокупность неравенств
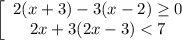
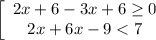
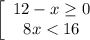

Отсюда х ≤ 12 или x∈ (-∞; 12]
8. 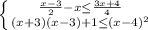
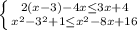

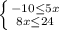

Отсюда -2 ≤ х ≤ 3 или x∈ [-2; 3]
a больше либо равно sqrt(7)-1
Пошаговое объяснение:
2^x=y. Заметим , что у должно быть больше 0
у^2-ay-a+3=0
у^2-ay+a^2/2=a^2/2+a-3
(y-a/2)^2=a^2/2+a-3
Решения есть если a^2+2a-6 больше либо равно 0
иначе (а+1)^2 больше либо равно 7
a больше либо равно sqrt(7)-1
или а меньше либо равно -sqrt(7)-1
Однако, требуется , чтобы у был больше 0.
у=а/2+sqrt(a^2/2+a-3)
или у=а/2-sqrt(a^2/2+a-3)
если а меньше 0, то второй корень не возможен.
Первый корень при отрицательном а
возможен только если sqrt(a^2/2+a-3)>-а/2
если а меньше либо равно -sqrt(7)-1 это не возможно.
Значит рассматриваем только случай
у=а/2+sqrt(a^2/2+a-3) и a больше либо равно sqrt(7)-1
Если a больше либо равно sqrt(7)-1 у положителен.
Пошаговое объяснение:
1/2x-2/7x=157/14x-4/14x=153x/14=153x=15*143x=210x=210/3x=70