Неравенство ax² + bx + c < 0 не будет иметь решений, если парабола
y = ax² + bx + c будет расположена над осью Ох или будет касаться оси.
Для этого коэффициент а должен быть положительным, а уравнение ax² + bx + c = 0 не должно иметь корней или иметь один корень, т.е. дискриминант должен быть меньше либо равен нулю:
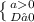
(p - 1) x² + (p - 2) x + 3p - 1 < 0
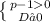
D = (p - 2)² - 4(p - 1)(3p - 1) = p² - 4p + 4 - 12p² + 16p - 4 = - 11p² + 12p
- 11p² + 12p ≤ 0
p(11p - 12) ≥ 0 (см. рис. 1)
p ∈ (- ∞ ; 0] ∪ [12/11 ; + ∞)
p > 1
(см. рис. 2)
p ∈[12/11 ; + ∞)
А1. х / 2.4 = 6 / 1.5
x = 2.4 / (6 / 1.5)
x = 2.4 / 4
х = 0.6
А2. х/4.2 = 5.1 / 1.7
x = (5.1 / 1.7) * 4.2
x = 3 * 4.2
x = 12.6
A3.
Длина окружности находится как произведение 2*pi*r, где r - радиус окружности, а pi - число пи, приблизительно равное 3.14
Lокр = 2 * 3.14 * 6 = 37.68
ответ: 3.
А4.
Площадь круга находится как произведение pi * r * r
Sкруга = 2 * 3.14 * 5 * 5 = 78.5
ответ: 4.