8
Пошаговое объяснение:
Первый - по формуле площади треугольника, вершины которого заданы координатами
1) А (-2; 0)
2) В (0; 4)
3) С (2; 0)
S = 1/2 · I(х₂-х₁)·(у₃-у₁) -(х₃-х₁)·(у₂-у₁)I
S = 1/2 · I(0-(-2))·(0-0) -(2-(-2))·(4-0)I =
= 1/2 · I0 - 4 · 4I = 1/2 · 16 = 8
ответ: 8
Второй - по формуле Герона (через длины сторон)
А (-2; 0)
В (0; 4)
С (2; 0)
АВ = √(0-(-2))²+(4-0)² = √(2²+4²) = √(4+16) = √20
ВС = √(2-0)²+(0-4)² = √(2²+4²) = √(4+16) = √20
АС = √(2-(-2))²+(0-0)² = √4² = 4
p = (√20 +√20+4) : 2 = √20 + 2
S = √ (p · (p-a)·(p-b)·(p-c))
S = √ ((√20 + 2) · (√20 + 2 - √20)·(√20 + 2 - √20)·(√20 + 2 - 4)) =
= √ ((√20 + 2) · 2 · 2 ·(√20 + 2 - 4)) =
= √ (4 · (√20 + 2) · (√20 - 2)) =
= √ (4 · (20 - 4)) = √ (4 · 16) = √ 64 = 8
ответ: 8
1рабочий=50дней
2рабочий=75дней
Пошаговое объяснение:
1р+2р=30 дней
1р+2р=6 дней
1р отдельно +40дней
1р–?
2р–?
Возьмём всю работу за 1 целую часть. Если за 30 дней рабочие выполняют 1 целую часть работы, то за 6 дней они выполнят 6/30=1/5 часть работы.
Тогда первому рабочему одному предстояло выполнить
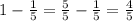
части работы, которая составила 40 дней
Пусть вся его часть работы =х, тогда:
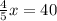
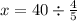
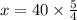
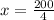
х=50
Итак: первому рабочему, работая отдельно, на выполнение всей работы понадобилось 50 дней.
Так как вся работа =1, тогда выполняя работу совместно их производительность= 1/30, тогда производительность 1 рабочего=1/50.
Найдём производительность второго рабочего:
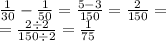
- это производительность 2-го рабочего, тогда он потратит времени, работая один:
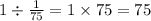
75 дней
Итак: каждый работая отдельно потратит: 1раб–50дней, 2раб=75дней
будет 30,восемь раз сложи или умножь 3,75 на 8