Умножение комплексных чисел в тригонометрической форме производится так:
z1 · z2 = |z1| · |z2| · (cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2)).
Подставляем данные:
z1 · z2 = 12*6*(cos(271° + 151°) + i sin(271° + 151°)) =
= 72(cos422° + isin422°) = 72(cos62° + isin62°).
По правилам аргумент комплексного числа записывается в радианах.
z1 · z2 = 72(cos(62°*π/180°) + isin(62°*π/180°) =
= 72(cos(31*π/90) + isin(31*π/90).
Это же число в алгебраической форме:
z = 29,10723689 + i*54,74275076.
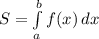
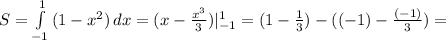
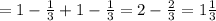 ед².
ед².