ответ:
пошаговое объяснение:
1) 30-200/n=25; домножим все на n: 30n-200=25n
с буквами влево, без букв вправо переносим с противоположным знаком: 30n-25n=200=> 5n=200. делим на коофициент при неизвестном, т.е на 5 => n=40
Пошаговое объяснение:
Задача №1.
Я, если честно, не понимаю формулировку "запиши ответ между корнями".
Но зато я попробую тебе решить данное уравнение.
Воспользуемся дискриминантом.
Вот формула:
x1,2 = ±b ± 
/2а
Где: b - второй коэффициент(который мы берем с противоположным знаком); а - это первый коэффициент(он же старший коэффициент); с - свободный член.
Подставим данные:
x1,2 = 7 ±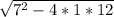
/2*1 = 7 ±1/2
Тогда:
x1 = 4
x2 = 3
Задача №2
Ну для начала 7 умножим на 2 и получим 14.
Тогда имеем:
2^2 - 14 + 12.
От нас требуется извлечь корень из этого выражения.
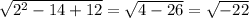- задача решения не имеет, т.к. корень из отрицательного числа извлекать нельзя.
Задача №3.
2 в квадрате = 4
Получили:
x^2 - 7x + 12 = 4
Переносим все вправо с изменением знака на противоположный.
x^2 - 7x + 8 = 0
Используя дискриминант, получаем следующие корни:
x1 =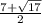 
x2 = 7 - корень из 17 поделить на 2
ответ:
пошаговое объяснение:
0 - 200/n = 25;
значения с х оставляем на том же стороне, а все остальные числа перенесем на противоположную сторону. при переносе любых значений и чисел на другую сторону уравнения, их знаки всегда меняются на противоположный знак, который у них был до переноса.
30 - 25 = 200/n;
200/n = 5;
5 * n = 200;
n = 200/5;
n = 40;
ответ: n = 40.
2) t * 20 - 36 = 144;
20 * t = 144 + 36;
20 * t = 140 + 30 + 4 + 6;
20 * t = 170 + 10;
20 * t = 180;
2 * t = 18;
t = 18/2;
t = 9;
ответ: t = 9.