"На одной Грани двугранного угла взято две точки, которые удалены от ребра на 34 см и 51 см. Расстояние Первой точки от Второй Грани 15 см. Найдите расстояние Второй точки от Грани."
Пошаговое объяснение:
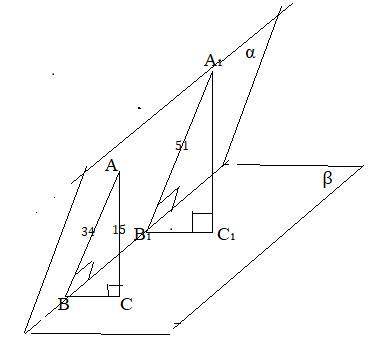
Дано α∩β=ВВ₁ , А∈α А₁∈α, С∈β, С₁∈β, АВ⊥ВВ₁ , А₁В₁⊥ВВ₁ ,АВ=34 см, А₁В₁=51 см , АС⊥β , АС=15см , А₁С₁⊥β
Найти А₁С₁
Решение.
1)Т.к АВ⊥ВВ₁ , А₁В₁⊥ВВ₁ , то и ВС⊥ВВ₁ , В₁С₁⊥ВВ₁ по т. о трех перпендикулярах ⇒∠АВС=∠А₁В₁С₁ как линейные углы одного двугранного.
2) Т.к АС⊥β , А₁С₁⊥β , то ∠АСВ=∠А₁С₁В₁=90°.
3)ΔАСВ=ΔА₁С₁В₁ по двум углам :∠АСВ=∠А₁С₁В₁ и ∠АВС=∠А₁В₁С₁. В подобных треугольниках сходственные стороны пропорциональны АВ:А₁В₁=АС:А₁С₁ или 34:51=15:А₁С₁ или А₁С₁=22,5 см
1
Пошаговое объяснение:
пусть в классе 30 учеников, тогда 60/30=2(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наибольшее число учеников без Маши
30+1=31 - это наибольшее число учеников с Машей
пусть в классе 10 учеников, тогда 60/10=6(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наименьшее число учеников без Маши
10+1=11 - это наименьшее число учеников с Машей
учеников не менее 10 и конфет не более 60 - решение соответствует условию задачи
1
Пошаговое объяснение:
пусть в классе 28 учеников, тогда 56/28=2(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наибольшее число учеников без Маши
28+1=29 - это наибольшее число учеников с Машей
пусть в классе 14 учеников, тогда 56/14=4(так как Маше половину своих конфет отдала её подруга, следовательно, число должно получиться чётное) - это наименьшее число учеников без Маши
14+1=15 - это наименьшее число учеников с Машей
учеников не менее 10 и конфет не более 60 - решение соответствует условию задачи
1/3+(-1/2) = 2/6 - 3/6 = -1/6
2 5/12+(-17 3/8) = 2 10/24 - 17 9/24 = -14 23/24
-29+17 1/8 = -11 7/8
17+(-1,25) = 17 - 1,25 = 15,75
-2 3/5+(-7 3/10) = -2 6/10 - 7 3/10 = -9 9/10
4 3/4+(-4 11/12) = 4 9/12 - 4 11/12 = -2/12 = -1/6