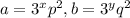 , где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на
, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 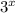 , получим уравнение
, получим уравнение 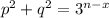 . Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на
. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 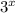 , имеем
, имеем 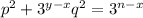 . Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
Можно, конечно, обыкновенные дроби перевести в десятичеые, а затем выбрать два нужных значения из прмежутка. Однако поступим по-другому. Найдём разницу между двух дробей, а потом будем к меньшей дроби прибавлять часть найденной разницы.
Для первого числа возьмём число в два раза меньшее, т.е. 1/9:
Для нахождения второго числа умножим числитель и знаменатель на 2, это будет тоже самое число. Затем числитель уменьшим на 1.
Вот это число и прибавим:
Или,
Отсюда тоже видно, можно выбрать минус 0,5; или -0,6; -0,55