Пошаговое объяснение:
а) Первый Пусть из некоторого города A нельзя попасть в некоторый город B по железной дороге. Рассмотрим множество M всех городов, в которые можно попасть из города A по железной дороге. Множество городов, не входящих в M, обозначим N. Множество N непусто, поскольку в нём содержится город B. Ясно, что из городов множества M нельзя попасть в города множества N по железной дороге.
Докажем, что из каждого города в любой другой можно попасть авиарейсами.
Если один из городов принадлежит M, а другой – множеству N, то между ними есть прямая авиалиния.
Пусть два города принадлежат M. Тогда из первого города можно попасть авиарейсом в некоторый город множества N, а оттуда (также самолётом) – во второй город.
Аналогично рассматривается случай, когда оба города принадлежат N.
Второй См. г).
б) См. в).
в) Пусть для города X это не так: есть город A, в который из X нельзя долететь за два "хода", и город B, в который из X нельзя доехать на поезде за два "хода" (значит, X и B связаны авиалинией). Пусть A и B связаны авиалинией. Тогда в X из A в можно добраться по воздуху с пересадкой в B. Противоречие.
Аналогично к противоречию приводит и предположение о том, что A и B связаны железной дорогой.
г) Пусть из A в нельзя долететь за три "хода", а из C в D нельзя доехать на поезде за три "хода". Тогда A и B связаны железной дорогой, а C и D – авиалинией.
Пусть A и C связаны железной дорогой. Тогда B и D связаны авиалинией (иначе был бы ж/д маршрут CABD), а A и D – железной дорогой (иначе есть авиамаршрут BDA). Противоречие: есть ж/д маршрут CAD.
Аналогично к противоречию приводит и предположение о том, что A и C связаны авиалинией.
Вычислим для начала область определения функции: функция существует когда знаменатель дроби не обращается к нулю
ООФ: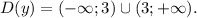
Упростим функцию:
Графиком функции есть прямая, проходящая через точки (0;1), (-1;-1)
Функция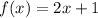
не имеет общих точек с прямой 
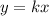в том случае, когда прямая 
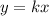будет проходить через выколотую точку (3;7), т.е. подставляя их координаты, мы получим
Если приравнять функции, т.е.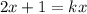
, тогда
То при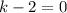
откуда 
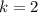графики функций общих точек не имеют. Если понять как графически делать, то очевидно, что если две прямые параллельны, то графики не имеют общих точек, а прямые параллельны в том случае, когда их угловые коэффициенты равны, т.е. k = 2
ответ: пр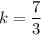и
и 