42)
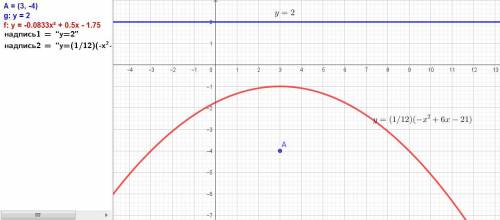
Дано: точка A(3;− 4) и прямая y = 2. Необходимо составить уравнение геометрического места точек, равноудаленных от заданной точки.
Пусть точка, соответствующая заданным требованиям, М(х; у).
Расстояние АМ² = (х - 3)² + (у - (-4))² = (х - 3)² + (у + 4)².
Так как по заданию расстояние АМ равно (2 - у), то подставим это значение в уравнение.
(2 - у)² = (х - 3)² + (у + 4)². Раскроем скобки.
4 - 4у + у² = х² - 6х + 9 + у² + 8у + 16. Приводим подобные.
12 у = -х² + 6х - 21.
ответ: у = (-1/12)х² + (1/2)х - (21/12). Это уравнение параболы.
Даны точки: А(1; -1; 8), В(-4; -3; 10) и С(-1; -1; 7).
Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA
= 0 .
Подставим данные и упростим выражение:
x - 1 y - (-1) z - 8
(-4) - 1 (-3) - (-1) 10 - 8
(-1) - 1 (-1) - (-1) 7 - 8
= 0.
x - 1 y - (-1) z - 8
-5 -2 2
-2 0 -1
= 0 .
(x - 1) (-2·(-1)-2·0) - ( y - (-1)) ((-5)·(-1)-2·(-2)) + (z - 8) ((-5)·0-(-2)·(-2)) = 0 .
2 x - 1 + (-9) y - (-1) + (-4) z - 8 = 0 .
ответ: 2x - 9y - 4z + 21 = 0.
Есть развёрнутая формула для определения уравнения плоскости по трём точкам:
(x-x1)*(у2-y1)*(z3-z1) – (x-x1)*(z2-z1)*(y3-y1) – (y-y1)*(x2-x1)*(z3-z1) + (y-y1)*(z2-z1)*(x3-x1) + (z-z1)*(x2-x1)*(y3-y1) – (z-z1)*(y2-y1)*(x3-x1) = 0.