y = -x-6
Пошаговое объяснение:
Касательная является параллельной другой прямой, если углы их наклона совпадают.
Если Вам известно понятие производной функции в точке, то можно использовать её геометрический смысл: производная в точке равна тангенсу угла наклона касательной в данной точке.
Так, например, наклон функции y=-x+2 одинаков во всех точках и равен -1, т.е. y' = -1.
Необходимо найти такие точки, принадлежащие y=x+2/x-2, в которых производная этой функции была бы равна -1.
Найдём производную: y' = 1 - 2/x^2.
Приравняем производную к -1: 1 - 2/x^2 = -1;
Отсюда следует, что x = ±1 -- это абсциссы точек, в которых производная функции равна -1.
Значения y для этих точек 1 и -5, т.е. точки (1, 1) и (-1, -5).
Касательной к графику функции y = x+2/x-2 в точке (1, 1) является прямая y = -x + 2, которая задана в условии. В точке (-1, -5) касательной является прямая y = -x - 6.
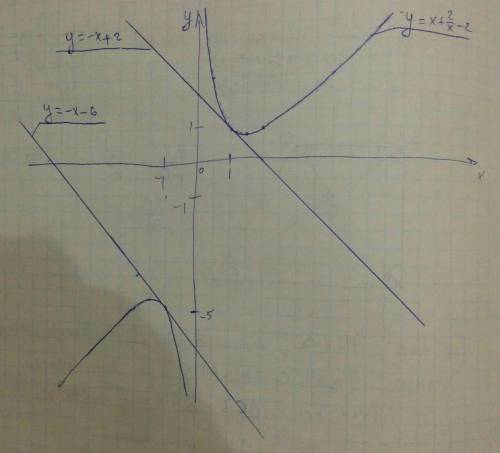
Если Вам неизвестно понятие производной, то просто постройте график данных функций и найдите экспериментально линейкой ту точку, в которой касательная будет параллельна y = -x + 2.
Построение в приложении.
Составим небольшое краткое условие:
5 часов утра - начало пути
2 часа ловил рыбу - не двигался!
10 часов утра - конец пути.
Скорость по течению 6+2=8 км/ч. Скорость против течения 6-2=4 км/ч.
Значит рыболов был в пути 10-5=5 часов
Из этих 5 часов он 2 часа ловил рыбу, т.е. плавал он 5-2 =3 часа.
Обозначим время, которое рыболов плыл по течению за х часов, тогда против течению он плыл (3-х) часов. Составим уравнение
8х=4(3-х)
8х=12-4х
8х+4х=12
12х=12
х=1
Значит рыболов по течению плыл 1 час, тогда против течения 3-1=2 часа.
Теперь найдем на какое расстояние он отплывал. Для этого умножим скорость на время, которое он находился в пути(если по течению, то берем скорость по течению и время по течению).
8*1=8 км.
ответ: 8км.
4 -4
-15 15
1/4 -1/4
0 0
1/3 -1/3
-8 8
3/4 -3/4
-2 2