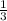часть всех запасов сахара для дрессуры, то у него осталась 
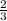запасов сахара для дрессуры, т.е. в 
раза больше, чем он потратил. Поскольку 
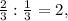или иначе говоря, поскольку 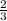вдвое больше, чем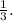 
кусков сахара.
недели.
недель.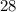
кусков сахара за недели, а значит, в неделю он тратил в два раза меньше, т.е.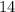 
кусков сахара в неделю.
кусков сахара в неделю.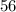
кусков после начальной дрессуры, то при расходе кусков сахара в неделю ему хватит этого остаточного запаса на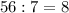 
недель.
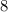недель.
5/6 >5/8,_ 17/30< 2/3,_ 79/68 >5/113,_ 11/12 < 19/20,_ 2³/₁₆ < 2⁹/₁₆
Пошаговое объяснение:
1) При сравнении дробей с одинаковым числителем больше та дробь, знаменатель которой меньше.
5/6> 5/8 ( На чем больше частей делится что-то, тем меньше получится каждая часть).
2) 17/30 и 2/3 приведем к общему знаменателю:
17/30 <20/30 ( при сравнении дробей с равными знаменателями больше та, у которой больше числитель. Если что-то разделить на 30 частей , то 17 частей меньше. чем 20 таких же).
3) 79/68 и 5/113
Первое число - неправильная дробь, оно больше едииницы. Второе - меньше единицы. Поэтому
79/68 > 5/113
4) 11/12 и 19/20
Первому числу до целого недостает 1/12, второму 1/20.
Т.к. 1/12> 1/20, то 19/20>11/12 ( см. объяснение п. 1)
5) Из смешанных чисел с равной целой частью больше та, у которого больше дробная часть. 2=2, 9/16>3/16, поэтому 2 целых и 3/16 меньше, чем 2 целых и 9/16.
(12+S-6)÷x=6; S+6=6x; S=6x-6
Для второго курьера:
(S-12+6)÷y=6; S-6=6y; S=6y+6
Приравняем по пути и выделим х :
6х-6=6у+6; 6х-6у=12; х-у=2; х=у+2
Составим уравнение времени до первой встречи, и так как время в пути у них было одинаковое уровняем:
(S-12)÷х=12÷у
Теперь подставим найденные значения S и х :
(6у+6-12)÷(у+2)=12÷у
у(6у+6-12)=12(у+2)
6у²-18-24=0
у²-3у-4=0
D=25
у₁=-1 не подходит,т.к. скорость не может быть отрицательной.
у₂=4 км/ч скорость второго курьера.
х=4+2=6 км/ч скорость первого курьера.
S=6×4+6=30 км расстояние от А до В.
ответ: 30 км расстояние от А до В ; 6 км/ч скорость первого курьера ; 4 км/ч скорость второго курьера.