y"-y'-6y=5e³ˣ
характеристическое уравнение для однородного к²-к-6=0; по Виета к=3; к=-2
Общее решение однородного уо.о.=с₁*е³ˣ+с₂е⁻²ˣ
Т.к. к=3 является корнем характеристического уравнения, то частное решение неоднородного уравнения по виду правой части имеет такой вид уч.=а*х*е³ˣ, найдем производные уч.'=ае³ˣ+3хае³ˣ=
ае³ˣ(1+3х); уч.''=3ае³ˣ(1+3х)+3ае³ˣ=6ае³ˣ+9ахе³ˣ
подставим у, у', у'' в уравнение. 6ае³ˣ+9ахе³ˣ-ае³ˣ-3хае³ˣ-6а*х*е³ˣ=5е³ˣ
6а+9ах-а-3ха-6а*х=5
5а=5⇒а=1; уч.=х*е³ˣ. тогда общее решение неоднородного равно сумме общего решения однородного и частного решения неоднородного, т.е. У*=х*е³ˣ+с₁*е³ˣ+с₂е⁻²ˣ
400
Пошаговое объяснение:
Решил Мудrost
Пусть х- это задуманное число.
Раз половина задуманного числа на 120 больше одной пятой задуманного числа,то одна пятая числа на 120 меньше чем половина задуманного числа, значит чтобы получилось равенство между (1/2)х и (1/5)х, нужно к (1/5)х прибавить 120, а (1/2)х оставить.У нас получается равенство(уравнение).
Составим и решим уравнение:
(1/2)х=120+(1/5)х
(1/2)х оставляем, а (1/5)х переносим влево поменяв знак на противоположный(-):
(1/2)х-(1/5)х=120
Приводим дроби (1/2)х и (1/5)х к общему знаменателю (10):
Получаем:
(5/10)х-(2/10)х=120
Раз дроби с одинаковым знаменателем, то их можно вычитать и складывать, в нашем случае их нужно вычесть:
(3/10)х=120
Теперь, чтобы избавиться от (3/10) в левой части уравнения, нужно обе части уравнения поделить на эту дробь:
х=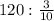
Меняем местами числитель (3) и знаменатель (10) у дроби 3/10 и число 120 делаем неправильной дробью 120/1 (Пояснение: единицу я не написал, потому что это не очень важно, она все равно в вычислениях не имеет значения) :
х=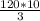
х=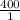
х=400
Пояснения знаков:
*-знак умножения
/-дробная черта
Ещё кое-что важное, я некоторые дроби с х(иксом, то есть неизвестным числом) взял в скобки чтобы показать что х(икс) находится не в знаменателе, а умножается на эту дробь.
Решил Мудrost
Маше выдали общественные деньги в сумме 165 рублей, ей надо было купить поздравительные открытки к 8 марта. В киоске были открытки по 3, 4, 5, 9 рублей. Маша решила купить открытки по одинаковой цене на всё сумму без сдачи. Сколько открыток могла купить Маша?
Решение:
165 делится на 5
165 (1+6+5=12) делится на 3
165 не делится на 9 и не делится на 4
следовательно Маша могла купить без сдачи только
165: 5 = 33 открытки по 5 рублей или
165:3 = 55 открыток по 3 рубля
вторую не придумала)