Задача на формулу полной вероятности и формулу Байеса.
Событие Н₁ - лампа из 1 партии, Н₂ - лампа из 2 партии, Н₃ - лампа из 3 партии.
Р(Н₁)=380/1000=0,38 , Р(Н₂)=270/1000=0,27 ,
Р(Н₃)=(1000-380-270)/1000=350/1000=0,35 .
Событие А - выбранная лампа бракованная -->
Р(А/Н₁) - вероятность того, что выбранная лампа бракованная принадлежит 1 партии, равна 4%, то есть Р(А/Н₁)=0,04 . Аналогично, Р(А/Н₂)=0,03 , Р(А/Н₃)=0,06 .
Вероятность выбора бракованной лампы ищем по формуле полной вероятности:
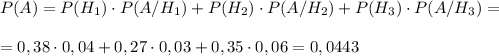
Вероятность того, что бракованная лампа из 2 партии ищем по формуле Байеса:
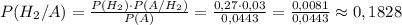
Дано: y = 2*x³ + 3*x² - 2
Пошаговое объяснение:
Первая производная. Y'(x) = 6*x² + 6*x = 6*x*(x + 1) = 0
Корни Y'(x)=0. Х₄ =-1 Х₅=0
Локальные экстремумы.
Максимум - Ymax( -1) = -1. Минимум - Ymin(0) = -2
Интервалы возрастания и убывания.
Возрастает Х∈(-∞;-1;]U[0;+∞) , убывает - Х∈[-1;0]
Дано: y = x⁴ - 2*x² + 3.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ -4*x = 4*x*(x-1)*(x+1) = 0
Точки экстремумов: x = 1, x = -1, x = 0
Локальные экстремумы: Ymin(-1) = Y(1) = 2 , Ymax(0) = 3
ответ:{-55}