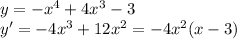
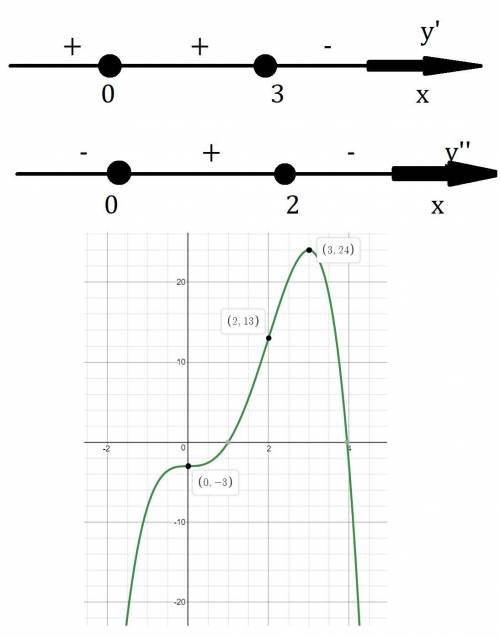
Как видно производная обращается в ноль при x=3 и x=0 это критические точки, используем метод интервалов, для определения знака производной на промежутках.
При x=0, производная не меняет знак, значит это не экстремум функции. При x=3, производная меняет знак с плюса на минус, значит это минимум функции.
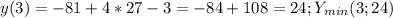
На (-∞;0)∪(0;3) функция растёт.
На (3;+∞) функция убывает.
Функция общего вида (не обладает чётность или нечётностью)
Найдём точки перегиба функции.
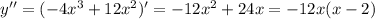
x=0 и x=2 это точки перегиба.
На (-∞;0)∪(2;+∞) функция выпукла вверх.
На (0;2) функция выпукла вниз.
Найдём координаты всего чего ещё не нашли.
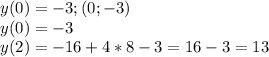
Можем строить.
Наименьшее значение (-∞;-∞) и (+∞;-∞)
Наибольшее значение (3;24)
дана эта формуланужно исследовать её на монотонностьнайти н" />
Пошаговое объяснение:
Задача №1
Не выполняя построения,
выяснить, принадлежит
ли точка А(6;1) графикам
уравнений
х -2у =4 и 2х + у = 5?
Задача №2
Построить в одной системе координат
графики уравнений у – 2х = 0 , у- 2х = 2 и
у -2х =-2.
ответьте на во Каково взаимное расположение графиков?
Чему равны угловые коэффициенты?
От чего зависит расположение графиков?
1.Выразим у через х.
2 Найти координаты двух точек ху
3 Отметить эти точки на координатной
плоскости и провести через них прямую.
Задача №3
Постройте графики уравнений в одной
системе координат: у-х-1=0 и у+х+1=0.
1.Выразим у через х.
х
2 Найти координаты двух точек у
3 Отметить эти точки на координатной
плоскости и провести через них прямую.
ответьте на во Каково взаимное расположение прямых?
Чему равны угловые коэффициенты?
Назовите координаты точки пересечения.
Задача №4
Каково взаимное расположение прямых?
ответ обосновать.
1)5х + 3=у и 2 +5х = у
2) 4-3х = у и 7 + 3х = у
3) 8х – у = 5 и 5 = -у +8х
Задача №5
Известно, что ордината некоторой точки
прямой, являющейся графиком уравнения
11х – 15у = 132, равна 0
Найдите абсциссу этой точки.
Р=18*2+5*2=36+10=46 см.
ответ: Периметр прямоугольника 46 см.