π/12 + (-1)^(n+1)•π/12 +πn/3, где n∈ Z.
Пошаговое объяснение:
cos3x = 1 + sin3x
cos3x - sin3x = 1
Разделим обе части равенства на √2, получим:
1/√2•cos3x - 1/√2•sin3x = 1/√2;
sin(π/4)•cos3x - cos(π/4)•sin3x = 1/√2
sin(π/4 - 3x) = 1/√2
sin(3x - π/4) = -1√2
3x - π/4 = (-1)^n•arcsin(-1/√2) + πn, где n∈ Z
3x = π/4 + (-1)^(n+1)•arcsin(1/√2) + πn, где n∈ Z
3x = π/4 + (-1)^(n+1)•π/4 + πn, где n∈ Z
x = π/12 + (-1)^(n+1)•π/12 + πn/3, где n∈ Z.
(Уравнение имеет вид
а•sinx + b•cosx = c.
Для его решения выполнено деление обеих частей равенства на число, равное √(а^2 +b^2).
В нашем случае а = -1, b = 1, √(а^2 +b^2) = √(1+1) = √2.)
Пошаговое объяснение:
1)Длина комнаты а= 6 м
найдем ширину комнаты ( b) :
b= 6 : 2= 3 м
Формула площади
S= a*b
S= 6*3= 18 м²
Площадь комнаты 18 м²
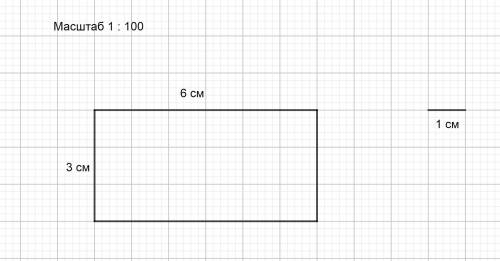
2) Масштаб 1 : 100 , т.е. 1 м на местности = 1 см на плане .
значит
6 м на плане будут равны 6 см , а
3 м на плане будут равны 3 см
рисунок во вложении
3) Периметр комнаты равен
Р= 2* (a+b)
P= 2*(6+3)= 18 м
Периметр комнаты на плане равен
Р= 2*(6+3)= 18 см
4) 1 м = 100 см
Значит
18 м = 18*100=1800 см
Найдем во сколько раз периметр комнаты больше периметра ее плана
1800 : 18 = 100 раз