Причины народных выступлений. Восстания 1868- 1869 гг. в Уральской и Тургайской областях. Административно-управленческие реформы, несмотря на отдельные их положительные стороны, усилили колониальную зависимость Казахской Степи. Под постройку крепостей изымались земли кочевников, широкомасштабно увеличивались налоги, а действия царских чиновников и перешедших на управленческую службу казахских феодальных групп обострили и без того трудное положение населения. Знать, начиная заниматься ростовщичеством, усилила административное давление на своих подчиненных. Для несостоятельных кочевников особенно неудобными были новые правила землепользования. Земли, занимаемые казахскими кочевьями, вопреки прежним юридическим документам и обещаниям правительства, были объявлены государственной собственностью.
Еще до реформы в Степи были введены государственные, земские сборы и повинности. Покибиточный сбор в размере 1 руб. 50 коп. серебром вырос до 3 руб. Обременительным был и билетный сбор, изымавшийся за работу и проживание в прилинейных русских селениях, и связанные с ним штрафные деньги. Другие поборы народ обозначил словом шыгын. Войскам обязаны были доставлять подводы. При этом со всеми видами сборов и повинностей были связаны различные злоупотребления.
Налог тяжелым бременем ложился на бедноту. С учетом земского сбора размер подати достигал 3 руб. 50 коп. Вновь, как и раньше, сбор был уравнительным — богатый и бедный платили одну сумму.
Надеюсь
1.Область определения функции: х ∈ R.
2. Нули функции. Точки пересечения графика функции с осью ОХ.
График функции пересекает ось X при f = 0
значит надо решить уравнение:
2 x + x^{3} - 3 x^{2} + 1 = 0.
Решение этого кубического уравнения даёт один действительный корень х = -0,32472.
3. Промежутки знакопостоянства функции:
y < 0, x ∈ (-∞; -0,32472),
y > 0, x ∈ (-0.32472; +∞).
4. Симметрия графика (чётность или нечётность функции).
Проверим функци чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
2 x + x^{3} - 3 x^{2} + 1 = - x^{3} - 3 x^{2} - 2 x + 1. - Нет
2 x + x^{3} - 3 x^{2} + 1 = - -1 x^{3} - - 3 x^{2} - - 2 x - 1. - Нет
значит, функция не является ни чётной, ни нечётной.
5. Периодичность графика - нет периодичности.
6.Точки разрыва, поведение функции в окрестностях точек разрыва, вертикальные асимптоты.
Так как функция не содержит дробей и корней, то точек разрыва нет.
7. Интервалы монотонности функции, точки экстремумов, значения функции в точках экстремумов.
Производная функции y' = 3x² -6x + 2.
Корни уравнения 3x² -6x + 2 = 0 равны 1 +- (√3/3).
Максимум функции равен 1 + (2/(3√3)) при х = 1 - (√3/3),
минимум равен 1 - (2/(3√3)) при х = 1 + (√3/3).
8. Интервалы выпуклости, точки перегиба.
Вторая производная равна: y'' = 6х - 6 = 6(x - 1).
Поэтому точка перегиба одна: х = 1, у = 1.
9. Поведение функции в бесконечности. Наклонные (в частности, горизонтальные) асимптоты.
Наклонную асимптоту можно найти, подсчитав предел функции x^3 - 3*x^2 + 2*x + 1, делённой на x при x->+oo и x ->-oo
\lim_{x \to -\infty}\left(\frac{1}{x} \left(2 x + x^{3} - 3 x^{2} + 1\right)\right) = \infty.
Предел равен ∞, значит, наклонной асимптоты слева не существует.
\lim_{x \to \infty}\left(\frac{1}{x} \left(2 x + x^{3} - 3 x^{2} + 1\right)\right) = \infty.
Предел равен ∞, значит, наклонной асимптоты справа не существует.
Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo
\lim_{x \to -\infty}\left(2 x + x^{3} - 3 x^{2} + 1\right) = -\infty.
Предел равен -∞.
Значит, горизонтальной асимптоты слева не существует.
\lim_{x \to \infty}\left(2 x + x^{3} - 3 x^{2} + 1\right) = \infty.
Предел равен ∞, значит, горизонтальной асимптоты справа не существует.
10. Дополнительные точки, позволяющие более точно построить график.
y(x)=x3−3x2+2x+1y(x)=x3−3x2+2x+1Таблица точек:
x y-2.0 -23 -1.5 -12.1 -1.0 -5 -0.5 -0.9 0 1 0.5 1.4 1.0 1 1.5 0.6 2.0 1 2.5 2.9 3.0 7 3.5 14.1 4.0 25
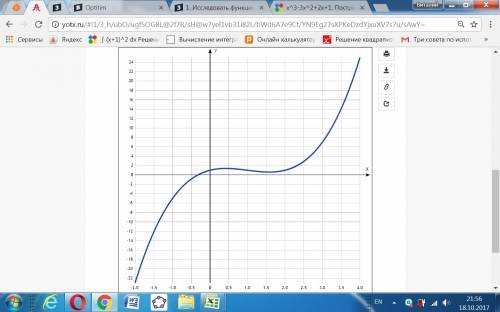
11. Построение графика функции по проведенному исследованию - дан в приложении.