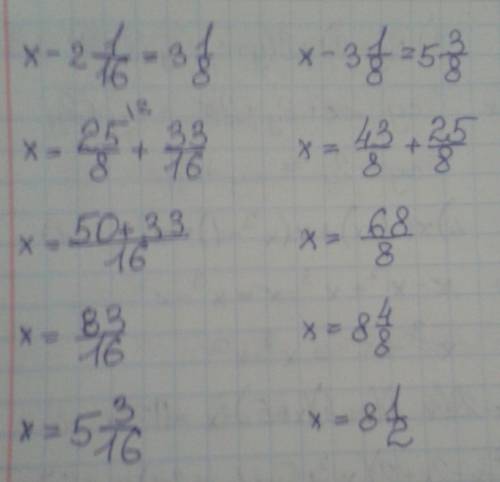
1) зачеркнули 7 из числа 17;
2) зачеркнули 8 из числа 85.
Решение 1:Искомое двузначное число представим в виде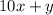 
(
и 
- однозначные и неотрицательные, при этом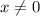 
).
1). Пусть зачеркнули цифру из разряда десятков. Тогда из числа 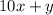получилось число . Нам нужно выполнение следующего равенства:
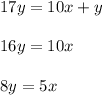
Единственные однозначные натуральные решения: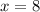 
и 
.
Значит, число 
⇒ 
.
2). Пусть зачеркнули цифру из разряда единиц. 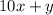⇒ . Уравнение составляется и решается по аналогии:
Откуда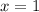 
и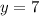 
.
Имеем второе подходящее решение: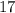 
⇒ 
.
Значит, двузначное число - это 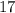или , или .
Можно было и кратким подбором решить, умножая все цифры на 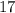(умножаемая цифра - та, которая могла остаться после вычеркивания), пока не станут появляться трехзначные числа.
Нам нужно, чтобы в получившемся числе присутствовало умножаемое число (иначе как оно смогло бы потом остаться?):
- не подходит, не двузначное.
- подходит, вычеркивали 
из числа .
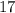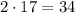- не подходит.
- не подходит.
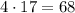- не подходит.
- подходит, вычеркивали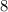 
из числа .
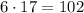- не подходит, начинаются трехзначные числа.
Получаем те же самые два решения: 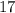и .
1. Выпадение герба и цифры при бросании монеты.
Событий всего два : либо герб, либо цифра.
Вероятность каждого события 1/2 = 0,5.
События равновозможные.
2. Попадание и промах при одном выстреле по мишени.
Событий всего два : либо попадание, либо промах.
Вероятности попадания и промаха 1/2 = 0,5.
События равновозможные.
3. Выпадение 1 и 5 при бросании игральной кости.
У кубика 6 граней. Вероятность выпадения любой из них 1/6.
Вероятность выпадения 1 равна 1/6.
Вероятность выпадения 5 равна 1/6.
События равновозможные.
4. Ровно одно попадание и хотя бы одно попадание при четырех выстрелах по мишени.
Исход каждого выстрела - либо промах (-), либо попадание (+) в мишень. Всего событий при четырёх выстрелах 2⁴ = 16.
Ровно одно попадание возможно в 4 случаях. Первый, второй, третий либо четвёртый выстрел в мишень, остальные три мимо : {+---}, {-+--}, {--+-}, {---+}. Вероятность 4/16 = 1/4.
Из 16 событий условию "хотя бы одно попадание при четырёх выстрелах" не удовлетворяет только событие "четыре промаха". Остальные 15 подходят под условие. Вероятность 15/16.
События НЕ равновозможные.
5. Появление карты красной и черной масти при вынимании одной карты из колоды
В любой колоде есть карты только двух цветов. Количество карт красной масти равно количеству карт чёрной масти. Поэтому вероятность достать карту определённого цвета одинакова.
События равновозможные.
ответ : 1, 2, 3, 5
