Укажите наибольшее натуральное число, кратное 5, удовлетворяющее неравенству: 127

👇

Увидеть ответ

Ответ:

еааа2платьев

22.08.2022

140, т.к. 140 делится на 5 и является натуральным числом.

4,4(25 оценок)

Открыть все ответы

Ответ:

romka1014

22.08.2022

№1.

30 - 17 = 13 девочек в классе

13/30 части класса - составляют девочки

13 - числитель; 30 - знаменатель.

№2.

а) 1 кг = 1 000 г

1 000 * 1/2 = 1000 : 2 = 500 г

1 000 * 3/5 = 1 000 : 5 * 3 = 600 г

б) 1 м = 100 см

100 * 1/4 = 100 : 4 = 25 см

100 * 7/10 = 100 : 10 * 7 = 70 см

в) 1 мин. = 60 сек.

60 * 1/6 = 60 : 6 = 10 сек.

60 * 2/3 = 60 : 3 * 2 = 40 сек.

№3.

2/3 к знаменателю 12:

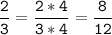
$\tt\displaystyle\frac{2}{3}=\frac{2*4}{3* 4}=\frac{8}{12}$

2/3 к знаменателю 15:

$\tt\displaystyle\frac{2}{3}=\frac{2*5}{3*5}=\frac{10}{15}$

2/3 к знаменателю 36:

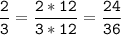
$\tt\displaystyle\frac{2}{3}=\frac{2*12}{3*12}=\frac{24}{36}$

К наименьшему общему знаменателю:

3/5 и 2/3:

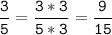
$\tt\displaystyle\frac{3}{5}=\frac{3*3}{5*3}=\frac{9}{15}\\$

$\tt\displaystyle\frac{2}{3}=\frac{2*5}{3*5}=\frac{10}{15}$

ответ: 9/15 и 10/15

3/4 и 5/16:

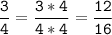
$\tt\displaystyle\frac{3}{4}=\frac{3*4}{4*4}=\frac{12}{16}\\$

ответ: 12/16 и 5/16

1/4 и 1/6:

$\tt\displaystyle\frac{1}{4}=\frac{1*3}{4*3}=\frac{3}{12}\\$

$\tt\displaystyle\frac{1}{6}=\frac{1*2}{6*2}=\frac{2}{12}$

ответ: 3/12 и 2/12.

№4.

41/100 нельзя сократить, т.к. 41 является простым числом, т.е. делится только на 1 и само себя.

Еще примеры несократимых дробей:

3/5; 13/20; 17/100; 23/50; 47/50; 107/200.

Сократим дроби:

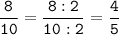
$\tt\displaystyle\frac{8}{10}=\frac{8:2}{10:2}=\frac{4}{5}\\$

$\tt\displaystyle\frac{12}{48}=\frac{12:12}{48:12}=\frac{1}{4}\\$

$\tt\displaystyle\frac{75}{100}=\frac{75:25}{100:25}=\frac{3}{4}\\$

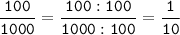
$\tt\displaystyle\frac{100}{1000}=\frac{100:100}{1000:100}=\frac{1}{10}$

№5.

Чтобы сравнить дроби, нужно привести их к общему знаменателю:

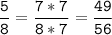
$\tt\displaystyle\frac{5}{8}=\frac{7*7}{8*7}=\frac{49}{56}\\$

$\tt\displaystyle\frac{4}{7}=\frac{4*8}{7*8}=\frac{32}{56}\\$

5/8 > 4/7 , т.к. 49/56 > 32/56

Правильная дробь всегда меньше неправильной:

7/10 < 10/7.

№6.

3 : 5 = 3/5

20 : 25 = 20/25 = 4/5

m : n = m/n

4,7(78 оценок)

Ответ:

EstrWite

22.08.2022

Давайте разберем данное выражение шаг за шагом:

1. Сначала решим выражение в скобках (6а+1/а-3):

В данном случае, у нас есть сложение дроби и числа. Для этого, нам нужно привести дробь к общему знаменателю. Общий знаменатель будет (а-3). Воспользуемся правилом сложения дробей с разными знаменателями:

(6а+1/а-3) = ((6а * (а-3)) + 1) / (а-3)

Далее, мы можем умножить 6а на а-3:

(6а * (а-3)) = 6а^2 - 18а

И теперь вместо (6а+1/а-3), мы можем написать:

((6а^2 - 18а) + 1) / (а-3)

2. Поработаем над вторым слагаемым: (6а-1/а):

Аналогично, приведем дробь к общему знаменателю, который будет равен а:

(6а-1/а) = ((6а * а) - 1) / а

(6а * а) = 6а^2

И теперь вместо (6а-1/а), мы можем написать:

((6а^2 - 1) / а)

3. Теперь, приступим к решению самого выражения:

а^2 - 9 / 2а^2 + 1 * ((6а^2 - 18а) + 1) / (а-3) + ((6а^2 - 1) / а)

В данном случае, нам нужно выполнить умножение и сложение.

Сначала умножим (6а^2 - 18а) на (а-3):

((6а^2 - 18а) + 1) * (а-3) = (6а^3 - 18а^2 + а - 3а^2 + 9а - 1) = (6а^3 - 21а^2 + 10а - 1)

Теперь мы можем заменить данное значение в выражении:

а^2 - 9 / 2а^2 + 1 * (6а^3 - 21а^2 + 10а - 1) / (а-3) + ((6а^2 - 1) / а)

В следующем шаге, нам нужно умножить (2а^2 + 1) на полученное значение:

(2а^2 + 1) * (6а^3 - 21а^2 + 10а - 1) = (12а^5 - 42а^4 + 20а^3 - 2а^2 + 6а^3 - 21а^2 + 10а - 1) = (12а^5 - 42а^4 + 26а^3 - 23а^2 + 10а - 1)

Заменяем данное значение в выражении:

а^2 - 9 / (12а^5 - 42а^4 + 26а^3 - 23а^2 + 10а - 1) / (а-3) + ((6а^2 - 1) / а)

И, наконец, мы можем сложить все общие числители:

а^2 - 9 + (12а^5 - 42а^4 + 26а^3 - 23а^2 + 10а - 1) / (а-3) + ((6а^2 - 1) / а)

Это и есть общий ответ на данное выражение.

4,5(44 оценок)

Это интересно:

Компьютеры-и-электроника

08.06.2020

Подробная инструкция: Как установить McAfee SiteAdvisor для Chrome...

Финансы-и-бизнес

10.05.2020

Как избежать ошибок в дейтрейдинге...

Хобби-и-рукоделие

18.12.2021

Как сделать кожаные браслеты своими руками: простые шаги для начинающих...

Семейная-жизнь