d²y/dx²=2*dy/dx
Можно переписать:
y"=2y' - это линейное однородное ДУ второго порядка с постоянными коэффициентами.
y"-2y'=0 (1)
Составим и решим характеристическое уравнение:
р²-2p=0
p*(p-2)=0
p₁=0
p₂=2
Получены два различных действительных корня, поэтому общее решение имеет вид:
y=C₁*e^(p₁*x)+C₂*e^(p₂*x), где p₁ и p₂ - корни характеристического уравнения, C₁ и C₂ - константы.
y=C₁*e^(0*x)+C₂*e^(2*x)
y=C₁+C₂*e^(2*x) - общее решение (2).
Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Наша задача состоит в том, чтобы найти такие значения констант С₁ и С₂, чтобы выполнялись оба условия.
Сначала используем начальное условие y(0)=3/2:
y(0)=C₁+C₂*e^(2*0)=C₁+C₂
Согласно начальному условию получаем первое уравнение:
C₁+C₂=3/2 (3)
Далее берем общее решение (2) и находим производную:
y'=(C₁+C₂*e^(2*x))'=0+2*C₂*e^(2*x)=2*C₂*e^(2*x)
Используем второе начальное условие y'(0)=1:
y'(0)=2*C₂*e^(2*0)=2*C₂
2*C₂=1
C₂=1/2 (4)
Теперь поддставим (4) в (3):
C₁+1/2=3/2
C₁=1 (5)
Остается подставить (4) и (5) в (2):
y=1+3/2*e^(2*x) - частное решение.
ответ: y=C₁+C₂*e^(2*x) - общее решение
y=1+3/2*e^(2*x) - частное решение
Подробнее - на -
Пошаговое объяснение:
Пошаговое объяснение:
I вариант решения
пусть прямая симметричная прямой y=-2x+3 имеет вид у=kx+b
найдем точки пересечения прямой y=-2x+3 с осями координат относительно оси ОУ
с осью ОХ у=0; -2x+3=0; 2x=3; x=1,5; (1,5;0)
с осью ОY x=0; y=3; (0;3)
так как прямые симметричны то
- они обе проходят через точку (0;3)
- симметричная прямая проходит через точку противоположную точке (1,5;0) точку (-1,5;0)
⇒ симметричная прямая проходит через точки (0;3) и (-1,5;0)
подставим координаты точки (0;3) в уравнение симметричной прямой у=kx+b координату точки (0;3)
получим 3=к*0+b; b=3
подставим координаты точки (-1,5;0) и значение b=3 в уравнение симметричной прямой у=kx+b получим
0=-1,5к+3 ; 1,5к=3; k=3/1,5=2
подставим b=1; k=2 в уравнение у=kx+b
у=2х+3
===============================================
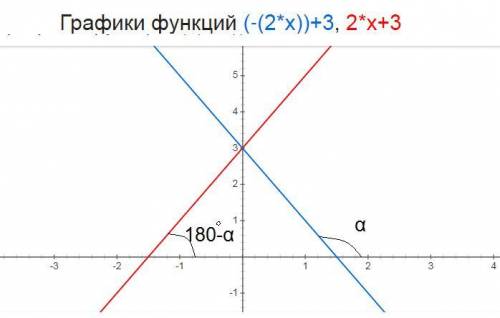
II вариант решения - тригонометрический
так как прямые симметричны то их углы наклона к оси ОХ будут в сумме давать 180°
так как tg(180°-а)=-tga то угловые коэффициенты симметричных прямых будут к₁ и к₂ противоположными числами а значение b₁ и b₂ будут одинаковыми так как обе прямые пересекают ось ОУ в одной точке ⇒ к₂=-к₁=-(-2)=2; b₂=b₁=3
уравнение прямой симметричной прямой y=-2x+3 относительно оси ОУ
у=2х+3
= 14х - 16 - 7 + 2,1х + 1,5х - 5 =
= 17,6х - 48.
17,6 * (-10/27) - 48 = -1472/27