есть два решения задачи:
Первый . Пусть Юля нальёт из полного малого кувшина озёрную воду в большой, а затем наполнит малый и из него дольёт большой доверху. Далее Юле надо опорожнить большой сосуд и вылить в него остаток из малого. Если малый был на 3 литра, то сейчас в большом 1 литр, иначе — 3 литра. Теперь пусть Юля снова попытается перелить воду из полного малого кувшина в большой. Если это ей удастся, то малый был трёхлитровым, если вода польётся через край, — четырёхлитровым.
Второй . Если бы у Юли большой кувшин вмещал 10 литров, то достаточно было бы попытаться налить в него воду из малого трижды. Если вода польётся через край, то малый на 4 литра, если нет, то на 3. С пятилитровым кувшином такая проверка возможна, если Юля опорожнит пятилитровый кувшин, когда тот заполнится.
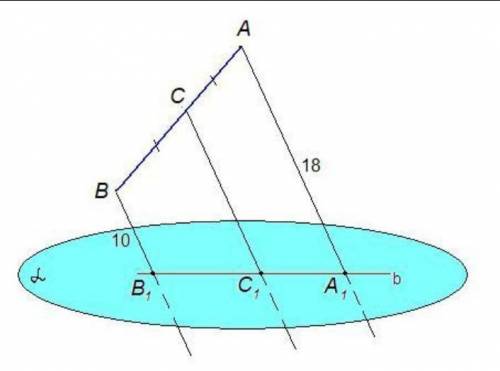
Через концы отрезка АВ и его середину С проведены параллельные прямые, которые пересекают некоторую плоскость α в точках А₁, В₁ и С₁ соответственно. Найти длину отрезка СС₁, если отрезок АВ не пересекает плоскость α и АА₁ = 18 см, ВВ₁ = 10 см.
14 см
Объяснение:
Параллельные прямые АА₁ и ВВ₁ задают плоскость, в которой лежит отрезок АВ и точка С, лежащая на нем.
В этой плоскости через точку С можно провести единственную прямую, параллельную АА₁, значит прямая СС₁ так же лежит в этой плоскости.
Плоскость (АВВ₁) пересекает плоскость α по прямой b, на которой лежат точки А₁, В₁ и С₁.
Итак, четырехугольник ABB₁A₁ - трапеция с основаниями АА₁ и ВВ₁.
СС₁ - средняя линия трапеции, а значит, равна полусумме оснований:
CC_1=\dfrac{AA_1+BB_1}{2}=\dfrac{18+10}{2}=\dfrac{28}{2}=14CC
1
=
2
AA
1
+BB
1
=
2
18+10
=
2
28
=14 см
6:22•100%=27%