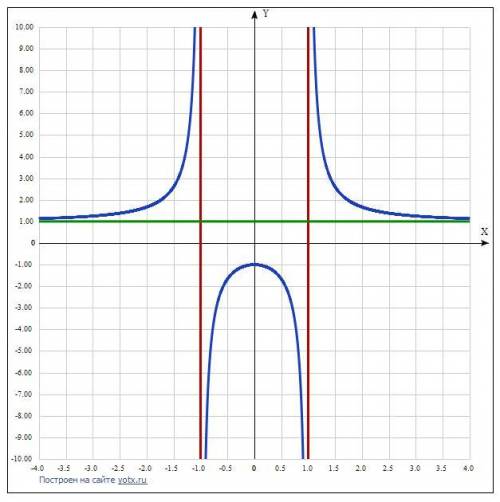
Дана функция y = (x^2 + 1)/(x^2 - 1).
1. Область определения функции - вся числовая ось: D(f) = R, x ≠ +-1.
Так как знаменатель дроби может обратиться в нуль при значениях x = 1 и х = -1, то из области определения функции эти 2 значения выпадают.
2. Функция f (x) = (x2 +1) /(x2-1) непрерывна на всей области определения кроме точек, в которых функция точно не определена (разрыв функции): x = 1 и х = -1.
Область значений функции приведена в пункте 8.
3. Точка пересечения графика функции с осью координат Оу:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в (x²+1) /(x²-1).
у = (0²+1)/(0²-1) = -1.
Результат: y = 0. Точка: (0; -1).
4. Точки пересечения графика функции с осью координат Ох:
График функции пересекает ось Ох при y=0, значит, нам надо решить уравнение:
(x²+1) /(x²-1) = 0.
Решаем это уравнение и его корни будут точками пересечения с Ох:
Для дроби достаточно приравнять нулю числитель:
x² +1 = 0,
x² = -1.
Результат: нет решения. График не пересекает ось Ох.
5. Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y^'=(2x(x^2-1)-2x*(x^2+1))/(x^2-1)^2 =(2x^3-2x-2x^3-2x)/(x^2-1)^2 =-4x/((x^2 -1)^2 )
Решаем это уравнение и его корни будут экстремумами (достаточно нулю приравнять числитель): -4x = 0.
Результат: х=0. Точка: (0; -1).
6. Интервалы возрастания и убывания функции:
С учётом двух точек разрыва функции и точки экстремума х = 0, имеем 4 интервала монотонности функции: (-∞; -1), (-1; 0), (0; 1) (1; +∞).
На промежутках находим знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -2 -1 -0,5 0 0,5 1 2
y' = 0,889 - 3,556 0 -3,556 - -0,889
Минимума функции нет.
Максимум функции в точке х = 0, у = -1.
Возрастает на промежутках: (-∞; -1) U (-1; 0).
Убывает на промежутках: (0; 1) U (1; +∞).
7. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y''=(4(3x² + 1))/(х² - 1)³ = 0.
Приравняем нулю числитель: 4(3x² + 1) = 0.
3x² + 1= 0.
3x² = - 1.
Это уравнение не имеет решения, поэтому у графика нет перегибов.
8. Асимптоты.
Асимтоты бывают трех видов: вертикальные, горизонтальные и наклонные.
а) Вертикальные асимптоты – есть в точках разрыва. Это линии х = -1 и х = 1.
б) Горизонтальная асимптота у графика функции определяется при нахождении предела функции на бесконечности:
lim┬(x→±∞)〖(x^2+1 )/(x^2-1)=(x^2/x^2 +1/x^2 )/(x^2/x^2 -1/x^2 )=1/(1-0)=1.〗
Таким образом, горизонтальная асимптота : у = 1.
С учётом максимума функции в точке (0; -1) и предела значения функции у = 1 определяем область значений функции:
у Є (-∞; -1] U (1; ∞).
в) наклонных асимптот нет. Функция f(x) имеет наклонную асимптоту y = k x + b тогда и только тогда, когда существуют конечные пределы k и в в уравнении у = kх + в.
〖 k=lim〗┬( x→±∞)〖(f(x))/x.〗
〖b=lim 〗┬( x→±∞)〖[f(x)-kx].〗
Для данной функции первый из этих пределов равен нулю, поэтому наклонная линия не определяется (она совпадает с горизонтальной асимптотой).
9. Четность и нечетность функции:
Проверим функцию - четна или нечетна с соотношений f(-x) = f(x) и -f(x) = -f(x). Итак, проверяем:
f(-x)=((-x)^2+1)/((-x)^2-1)=(x^2+1)/(x^2-1)=f(x).
3начит, функция является чётной.
10. Таблица точек.
x y
-4.0 1.133
-3.5 1.178
-3.0 1.25
-2.5 1.381
-2.0 1.667
-1.5 2.6
-1.0 -
-0.5 -1.667
0 -1
0.5 -1.667
1.0 -
1.5 2.6
2.0 1.667
2.5 1.381
3.0 1.25
3.5 1.178
4.0 1.133