Пошаговое объяснение:
Дана функция y = 3 * sin(x + П/6) - 2.
Область определения - все допустимые значения переменной x.
Значение переменной X здесь определяется областью определения функции y = sinx - вся числовая ось. Так как здесь к аргументу добавлено число П/6, то значения аргумента не меняются.
Значением синуса определенного угла (x +П/6) может быть число от -1 до 1. Напишем это:
-1 < sin(x + П/6) < 1;
Умножим все части неравенства на 3:
-3 < 3 * sin(x + П/6) < 3;
Ко всем частям неравенства прибавим -2:
-5 < 3 * sin(x + П/6) + 2 < 1.
Область значения функции - все числа от -5 до 1.
Пусть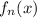 
означает 
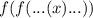, где 
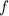применена 
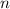раз.
Поскольку 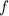многочлен, то у него есть значение в любой точке. (*)
Докажем утверждение по индукции.
База: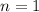 
- это то, что дано по условию.
Переход:
Пусть для некоторого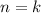 
верно; Докажем, что из этого следует справедливость утверждения и для 
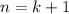; Действительно, по предположению индукции множество решений уравнения 
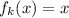совпадает с 
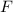; Возьмем 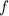от обеих частей (благодаря (*) мы можем это сделать): 
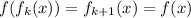; Но если сделать замену 
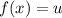, получим 
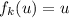; А множество решений этого уравнения лежит в 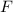; Предположим, что есть некоторый элемент 
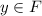, такой, что для него не найдется 
, чтобы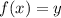 
; Тогда 
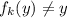, но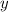 
лежит в 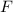, противоречие. Это завершает переход.
один угол х°
другой 2/3х°
х+2/3х=180
5/3х=180
х=180:5/3
х=108
108° - первый угол
180-108=72° - второй угол