Общее решение
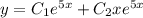
Частное решение
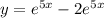
Пошаговое объяснение:
линейное однородное дифференциальное уравнение с заданными начальными условиями
y'' - 10y' + 25y = 0, y(0)=1,y'(0)=3
Запишем характеристическое уравнение k² - 10 ⋅ k + 25 = 0. Найдем его корни
k² - 10 ⋅ k + 25 = 0
k² - 2·5⋅ k + 5² = 0
(k - 5)² = 0
k₁ = k₂ = 5
Получили два совпадающих корня, следовательно, общее решение имеет вид
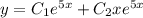
Для нахождения частного решения найдем производную функции
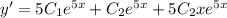
Подставляем начальные условия в функцию и ее производную
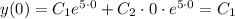
Из начальных условий у(0) =1
Следовательно С₁ = 1
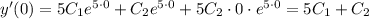
Из начальных условий y'(0)=3
Следовательно 5С₁ +С₂ = 3
С₂ = 3 - 5·1
С₂ = -2
Запишем частное решение уравнения
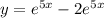
Дом 5 км 100 м Парк
> 300 м/мин ? (+5 м/с) <
1) 5 100 · 2 = 10 200 м = 10 км 200 м - проехал Костя от дома до парка и обратно;
2) 5 100 : 300 = 17 мин - время движения от дома до парка;
3) 300 м /мин = 300 м : 60 с = 5 м/с
5 + 5 = 10 м/с - скорость Кости на обратном пути;
5 100 : 10 = 510 с = (510 : 60) мин = 8 мин 30 с - время движения от парка до дома;
4) Масштаб 1 : 1 000 000 показывает, что 1 см на карте соответствует 1 000 000 см на реальной местности.
5 100 м = 510 000 см - расстояние в реальности
510 000 : 1 000 000 = 510 : 1 000 = 0,51 см = 5,1 мм - расстояние на карте.