Нехай Похила перетинає площину в точці B.
З точки а опустимо перпендикуляр до площини α в точку С, що належить площині. АС і буде відстанню від точки А до площини. ВС - проекція похилої.
У прямокутному трикутнику АВС відома гіпотенуза АВ, рівна 6 см, і кут в = 60 градусів. Знайдемо катети.
Кут в дорівнює 60 градусам, тоді кут А дорівнює 30.
Катет, що лежить проти кута А дорівнює половині гіпотенузи, значить
НД = 1/2*АВ = 1/2 * 6 = 3 см.
За теормеме Піфагора знаходимо другий катет
АС = √(АВ2-ВС2) = √(36-9) = √25 = 5,
Відповідь: 3 см - Довжина проекції, 5 см - відстань від точки А до площини.
Пошаговое объяснение:
3) Площадь круга: S=πR²
Измеряешь горизонтальную сторону прямоугольника и делишь ее на 2. Это значение -радиус(R).
Считаешь S= 3*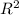
. Так мы нашли S круга.
Дальше находим площадь прямоугольника: S=ab
Умножаешь длину на ширину, узнаешь площадь прямоугольника.
Теперь из площади прямоугольника вычитаешь площадь круга, то есть
Площадь закрашенной фигуры равна:
S= ab - 3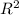
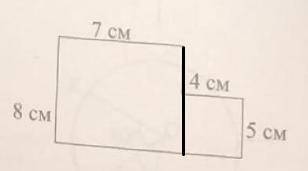
4) Фигура состоит из 2 фигур(см.картинку):
Из прямоугольника со сторонами 8 и 7.(Его площадь равна S=ab=56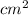
)
и прямоугольника со сторонами 4 и 5. (Его площадь равна S=ab=20)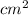
Площадь фигуры =76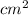=7600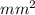 
D = n^2 - 4m*k < 0
4m*k > n^2 > 0
Произведение положительно, значит, m и k имеют одинаковые знаки.
4m + 2n + k > 0
4m + k > -2n
Возможны такие случаи:
1) n < 0, тогда -2n > 0
4m + k > -2n > 0; m и k оба > 0.
2) n > 0, тогда -2n < 0, но |-2n| < |4m + k|.
Например, |-2n| = 2, |4m + k| = 6.
Если при этом 4m + k > -2n, то 4m + k > 0; m и k оба > 0.
3) n > 0, -2n < 0 и |-2n| > |4m + k|.
Например, |4m + k| = 2, |-2n| = 6.
Если при этом 4m + k > -2n, то 4m + k > 0, m и k оба > 0.
Ситуации -2n = -6, n = -3, 4m + k = -2, m и k оба < 0, 4m*k = -p < 0
быть не может, тогда
D = n^2 - 4m*k = 3^2 + p > 0,
И тогда квадратное уравнение имеет решения.
ответ: m и k оба больше 0.