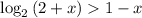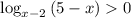Какое число надо вписать в окошко чтобы равенство ( ) —= 5 54 6 стало верным

Question

Математика: Какое число надо вписать в окошко чтобы равенство ( ) —= 5 54 6 стало верным

27Анютка27 · Accepted Answer

(I) ; (II) ; – строго монотонно возрастает ;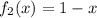 –  строго монотонно убывает ; 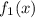Значит пересечение графиков функций и 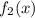– единственно. 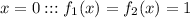Очевидно при – это и есть пересечение, после которого монотонно возрастающая функция строго превышает убыващую, что и требуется в уловии (I). 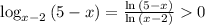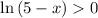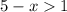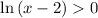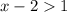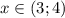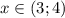Значит решение (I) ::: x 0 ; ; Значит или оба логарифма положительны, или оба отрицательны: (A) при , а значит x 4 ; (Б) при , а значит x 3 ; (А) и (Б) могут быть одновременно положительными при : 3 x 4 . Оба логарифма, очевидно,...

MOGZ ответил