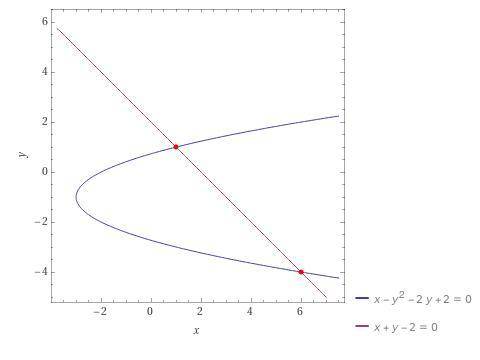
Даны уравнения кривой второго порядка x-y²-2y+2=0 и прямой x+y-2=0.
В уравнении кривой выделим полный квадрат.
x - (y² + 2y + 1) + 1 +2=0,
(y + 1)² = x + 3, приведём к каноническому виду.
(y - (-1))² = 2*(1/2)(x - (-3)).
Это уравнение параболы, ветви которой направлены вправо симметрично прямой у = -1, параллельной оси Ох, вершина в точке (-3; -1).
Точки пересечения с прямой находим решением системы.
{x-y²-2y+2=0
{x+y-2=0. x = 2 - у подставим в первое уравнение.
2 - у - y²- 2y + 2=0.
y² + 3y - 4 = 0. Д = 9 + 4*4 = 25.
х1 = (-3 + 5)/2 = 1, у1 = 2 - х = 2 - 1 = 1.
х2 = (-3 - 5)/2 = -4, у2 = 2 - х = 2 - (-4) = 6.
ответ: точки (1; 1) и (6; -4).
108/π см
Пошаговое объяснение:
1) Сторона правильного шестиугольника равна радиусу окружности, описанной около этого шестиугольника, так как:
- окружность 360° делится на 6 равных центральных углов (каждый из которых равен 360 : 6 = 60°);
- 6 образовавшихся треугольников являются равносторонними, т.к. две стороны каждого треугольника являются радиусами описанной окружности, в силу чего углы при основании равны (180 - 60) / 2 = 60°.
2) Длина выделенной линии L равна 18 радиусам описанной окружности R:
L = 18R
3) Длина окружности С и её радиус R связаны соотношением:
С = 2πR, откуда R при С = 12 см равен:
R = 12 : 2π = 6/π см
4) Находим длину выделенной линии L:
L = 18R = 18 · (6/π) = 108/π см ≈ 34,4 см
ответ: длина выделенной линии равна 108/π см, или ≈ 34,4 см.
468/26=18