В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.
В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.
Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.
Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.
Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.
Пошаговое объяснение:
Пошаговое объяснение:
для обоих случаев:
Площадь криволинейной трапеции - это определенный интеграл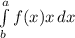 
для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
1)
f(x) = 6x -6x²; y=0; x=0; x=1
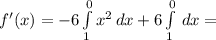
(-2x³) Ι₀¹ + 3x²Ι₀¹ = -2 +3 = 1
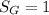
точки для построения графика
х=0; у= 0;
х= 0,2; у=0.96
х= 0,4; у = 1,44
х=0,6; у=1,44
х=0,8; у = 0,96
х = 1; у= 0
2)
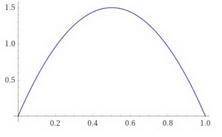
f(x) = х³ - 1; y=0; x=2; x=3
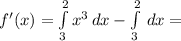
(х⁴/4) Ι₂³ + (-х) Ι₂³ = 65/4 -1 = 61/4
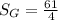
точки для построения графика
х=2; у=7
х=2,2; у = 9,65
х = 2,4; у=14,62
х=2,6; у=16,58
х=2,8; у=20,95
х=3; у=26
Графики на фото.
файл 11 - график f(x) = 6x -6x²; y=0; x=0; x=1
файл 22 - график f(x) = х³ - 1; y=0; x=2; x=3
2)9*3=27(км
3)27+14=41(км.)
ответ: туристы начали движение на расстоянии 41 км.