Собственно, вот в этой задаче я уже решал, но почему-то пропали прикреплённые картинки. По этой причине повторюсь.
Если принять сторону основания за a, a ребро за b, то в зависимости от расчёта приходим к одной из формул (они приводимы друг к другу):
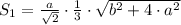
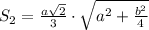
Сначала доказываете, что плоскость BMD перпендикулярна AC, далее - перпендикулярна A'C', A'C' пересекает BMD в точке P, ну и перпендикулярна всем прямым данной плоскости, проходящим через P => ND перпендикулярна A'C'.
Т.о. 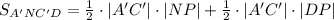
т.е. 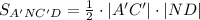
Найдём длины нужных нам в дальнейшем отрезков:
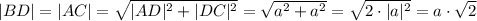
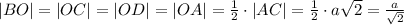
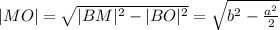
В треугольнике BMD DM и MO это медианы, пересекающиеся в точке P. Т.о. 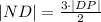
AC || A'C' из подобия треугольников AMC и A'MC' следует, что 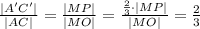
т.е. 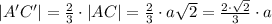
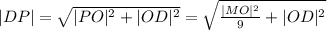
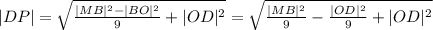
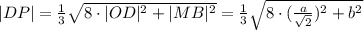
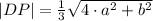
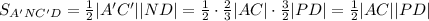
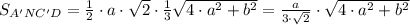
Теперь подставляем значения в формулу:
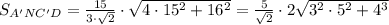
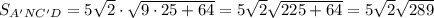
ответ: 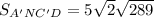
P.S.> Для примера - есть вариант, где a=6, b=12. В этом случае результат будет следующий:
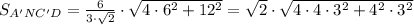
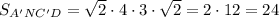
Это соответствует правильному ответу.
P.P.S.> Попробую прикрепить ещё снимки решения на бумаге (если получится) - там 2 варианта. Почему-то не всегда прикреплённые картинки сохраняются. По этому и вбил решение текстом.

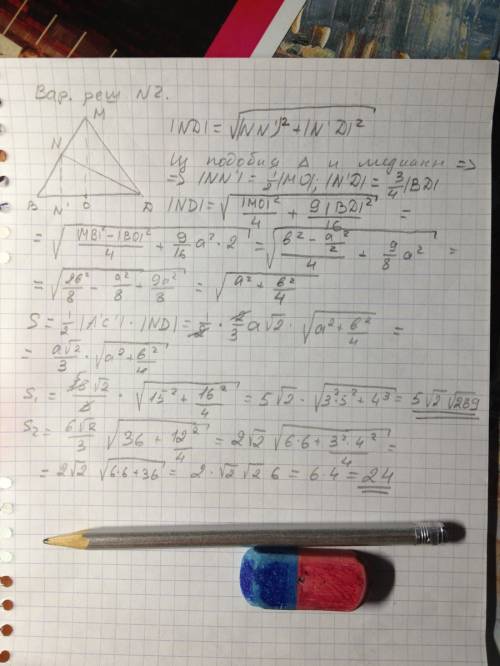
искомое сечение - симметричный четырехугольник BPKL
диагонали PL , BK пересекаются под углом 90 град
по условию
стороны основания AB=BC=CD=AD =4
боковые ребра MA=MB=MC=MD =8
точка К - середина ребра MD ; KD = MD /2 = 8/2=4
ABCD -квадрат
диагональ AC = BD = 4√2
пересечение диагоналей точка F : BF =FD = BD/2 =4√2 /2 =2√2
BK - медиана треугольника MBD
длина медианы BK = 1/2 √(2 BM^2 +2 BD^2 - MD^2 ) =1/2 √(2*8^2 +2*(4√2)^2 - 8^2 ) =4√2
по теореме косинусов
cos KBD = ( KD^2 - (BK^2+BD^2) )/ (-2*BK*BD)= ( 4^2 - ((4√2)^2+(4√2)^2) )/ (-2*4√2*4√2)= 3/4
MF - высота
треугольник EBF - прямоугольный
BE = BF / cos KBD = 2√2 / 3/4 = 8√2/3
KE = BK - BE =4√2 -8√2/3 =4√2/3
по теореме Пифагора EF =√(BE^2 - BF^2) =√( (8√2/3)^2 - (2√2)^2) =2√14/2
MF - высота
треугольник MFB - прямоугольный
по теореме Пифагора MF =√( MB^2 -BF^2) =√( 8^2- (2√2)^2 ) =2√14
ME =MF -EF =2√14 -2√14/2 = 2√14/2
треугольники MPL ~ MCA подобные
PL / AC = ME /MF ; PL = AC * ME /MF = 4√2 * 2√14/2 /2√14 =2√2
площадь сечения(четырехугольника BPKL)
Sс = PL*BK *sin<BEP /2 = 2√2*4√2*sin90 /2 = 8
ответ 8
ответ: 157
б) 95, 100... 160 делится на 5 (160-95)/5=13+1=14 чисел.
100, 125, 150 делятся на 25 (это 5^2) + 3 числа.
125 (это 5^3) + 1 число
14+1+3=18
Итого получаем что данное число делится на 5^18.
ответ: 5^18
в) произведение чисел 100, 110, 120, 130, 140, 150, 160 даёт как минимум 8 нолей на конце
произведение пар 95*102, 105*112,..., 155*162 даст как минимум 7 нолей на конце
8+7=15
ответ: 15 нолей