Пошаговое объяснение:
1)
Приводим подынтегральное выражение к виду:
x*(1-6x+12x^2-8x^3)=x-6x^2+12x^3-8x^4
По стандартным формулам ответ:
x^2/2-2x^3+3x^4-1,6x^5+C
2) Приводим подынтегральное выражение к виду:
1,5x^2-x+2,5
По стандартным формулам ответ:
0,5x^3-0,5x^2+2,5x+C
3) Приводим подынтегральное выражение к виду:
2x-e^(xln4)+e^(3x)
По стандартным формулам ответ:
x^2-(1/ln4)*4^x+(1/3)e^(3x)+C
4) ) Приводим подынтегральное выражение к виду:
3x^2,5-x^2+x^(-0,5)
По стандартным формулам ответ:
(6/7)x^3,5 (1/3)*x^3 +2*x^0,5+C
5) Приводим подынтегральное выражение к виду:
x^2+3x+4
По стандартным формулам ответ:
(1/3)*x^3+1,5x^2+4x+C
Всюду
C - любое число,x^а - х в степени а.
Пошаговое объяснение:
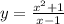
ОДЗ: х-1≠0 х≠1.
1) определим вертикальные асимптоты:
х=1.
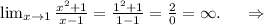
x=1 - вертикальная асимптота.
2) определим наклонные асимптоты:
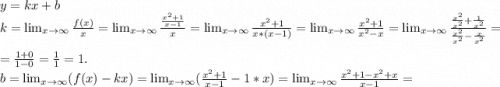
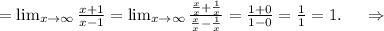
y=x+1 - наклонная асимптота.
ответ: х=1, у=х+1.
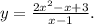
ОДЗ: х-1≠0 х≠1.
1) определим вертикальные асимптоты:
х=1.
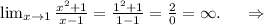
x=1 - вертикальная асимптота.
2) определим наклонные асимптоты:
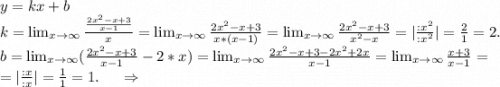
y=2x+1 - наклонная асимптота.
ответ: х=1, у=2х+1.
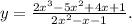
ОДЗ: 2x²-x-1≠0
2x^2-2x+x-1≠0
2x*(x-1)+(x-1)≠0
(x-1)*(2x+1)≠0
x-1≠0
x≠1
2x+1≠0
x≠-0,5.
1) определим вертикальные асимптоты:
x=1.
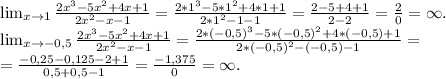
x=1 и х=-0,5 - вертикальные асимптоты.
2) определим наклонные асимптоты:
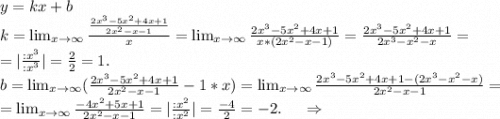
y=x-2.
ответ: x=1, x=-0,5, y=x-2.