Пошаговое объяснение:
Парабола является кривой, представляющей собой геометрическое место точек,
равноудалённых от фокуса параболы и другой заданной прямой. Эта кривая, а также
соответствующий ей в трёхмерном мире эллиптический параболоид, играют важную
роль во многих физических процессах, в связи с чем нашли широкое применение и
рас во многих инженерных, технических и др. устройствах, в
архитектуре. Парабола изображена на рисунке 1.
Парабола является линией конического сечения, открытие которых
приписывают Менехему. Учение о конических сечениях было развито Евклидом, а
также Аполлонием Пергским, который рассмотрел в своём труде все конические
сечения, а также их свойства, причём труды Аполлония примечательны тем, что они
представляют собой синтез аналитической и начертательной геометрии.
Важным свойством параболы является то, что любой предмет в поле тяготения
перемещается по параболе при отсутствии сопротивления воздуха или в условиях,
когда мы этим фактором можем пренебречь.
Наиболее значимым является т.н. «оптическое свойство» параболы - пучок
лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. Изза этого параболе нашли самые различные применения в различных оптических
устройствах, от ламп и до телескопов. В силу корпускулярно-волновой природы света,
оптические свойства параболы были переложены на составные части различных
радиопередающих устройств, например, узконаправленные, спутниковые антенны и
проч.
Такс, ну я попробую, хз что получится. Я так то в седьмом классе)
2. (пикчу прикрепил)
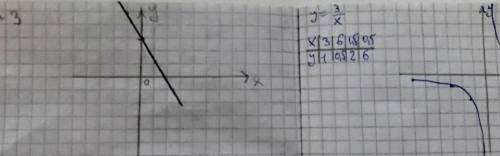
а) Это график обычно линейной функции
б) А это уже график обратной пропорциональности (гипербола)
3.
а) Возводим все в квадрат. 2 переносим.
x + 4 = x^2
Теперь чертим график y = x^2 (парабола) и график y = x + 4 (линейная функция). Точки пересечения - это и есть наши x. Если потом влом не будет, может нарисую.
б) Выносим x
x(x^2 + 2) + 3 = 0
3 переносим, делим все на x
x^2 + 2 = -3/x
Снова чертим график параболы (x^2 + 2) и гиперболы (-3/x). Находим точки пересечения, это и есть значение x. Думаю все это и сам умеешь, но опять же, может потом начерчу.
Напоминаю, что график гиперболы y = -3/x будет проходить в правой верхней (2) четверти и в левой нижней (4)!
4.
Выносим x
x(x + 5)
x ≠ 0 (т.к. на ноль делить нельзя).
x ≠ -5
Любое другое значение нас устраивает.
x ∈ (-∞; -5) v (-5; 0) v (0; +∞)
p.s. Извини, что так долго. Отвлечься пришлось)
ответ: 4
2) 192:48 = 4
ответ: 4
3) 648:72 = 9
ответ: 9
4) 352·46-5840:80 = 16 119
ответ: 16 119