НОД (Наибольший общий делитель) 240 и 264
Наибольший общий делитель (НОД) двух данных чисел 240 и 264 — это наибольшее число, на которое оба числа 240 и 264 делятся без остатка.
НОД (240; 264) = 24.
Как найти наибольший общий делитель для 240 и 264
Разложим на простые множители 240
240 = 2 • 2 • 2 • 2 • 3 • 5
Разложим на простые множители 264
264 = 2 • 2 • 2 • 3 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (240; 264) = 2 • 2 • 2 • 3 = 24
НОД (432; 792) = 72.
Как найти наибольший общий делитель для 432 и 792
Разложим на простые множители 432
432 = 2 • 2 • 2 • 2 • 3 • 3 • 3
Разложим на простые множители 792
792 = 2 • 2 • 2 • 3 • 3 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (432; 792) = 2 • 2 • 2 • 3 • 3 = 72
НОД (185; 205) = 5.
Как найти наибольший общий делитель для 185 и 205
Разложим на простые множители 185
185 = 5 • 37
Разложим на простые множители 205
205 = 5 • 41
Выберем одинаковые простые множители в обоих числах.
5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (185; 205) = 5 = 5
1) 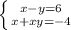
x-y=6
x=6+y 6+у+6у+у^2=-4
у^2+7у+10=0
у1= -2
у2= 5
х1= 6+2= 8
х2= 6-5 = 1
ответ: (8; -2) ; (1;5)
5) 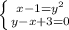
у-х+3=0
-х=-3-у
х= 3-у 3-у-1=y^2
-у^2-у+2=0
y^2+y-2=0
y1= 1
y2= -2
x1= 3-1 = 2
x2= 3+2 = 5
ответ: (2;1) ; (5;-2)
3) 
x-y=1
-y=1-x
y= x-1 x^2-2x+2-26=0
x^2-2x-24=0
x1= 6
x2= -4
y1= 6-1 = 5
y2= -4-1 = -1
ответ: (6;5) ; (-4; -1)
все что могу.