Пошаговое объяснение:
Обозначим через x км/ч скорость теплохода в неподвижной воде. Тогда, его скорость по течению равна x+2 км/ч, а против течения x-2 км/ч. Сначала теплоход идет по течению реки 80 км, на которые он затратил 80 : (х+2) часов. Затем, он стоит 3 часа, после чего движется в обратном направлении 80 : (х-2) часов. В сумме он затратил на весь путь 12 часов. Получаем уравнение:
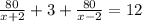
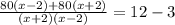
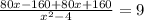
160x=9 * (x²-4)
160x=9x²-36
-9x²+160x+36=0
D=160²-4*(-9)*36 = 26896
√26896 = 164
x₁=(-160+164) / 2*(-9) = -2/9
x₂=(-160-164) / -18 = 18 км/ч
Так как скорость теплохода не может быть отрицательным числом, то получаем ответ 18 км/ч
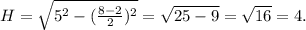
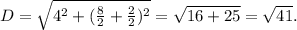
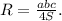
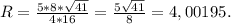
в четвертой четверти.