Логарифмический ноль. Элементарное свойство, которое нужно обязательно помнить. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.
Логарифмическая единица. Еще одно простое свойство: если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
Основное логарифмическое тождество. Отличное свойство, превращающее четырехэтажное выражение в простейшую b. Суть этой формулы: основание a, возведенное в степень логарифма с основанием а, будет равно b.
Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2х логарифмов, у которых будут одинаковые основания. И так невычислимые логарифмы становятся простыми.
Логарифм частного. Здесь ситуация схожая с суммой логарифмов. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.
Вынесение показателя степени из логарифма. Тут действуют целых 3 правила. Все просто: если степень находится в основании или аргументе логарифма, то ее можно вынести за пределы логарифма, в соответствии с этими формулами
Формулы перехода к новому основанию. Они нужны для выражений с логарифмами, у которых разные основания. Такие формулы в основном используются при решении логарифмических неравенств и уравнений.
Пошаговое объяснение:
1.41
Пошаговое объяснение:
Ну, пусть искомое число - это х,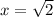 
. Тогда
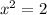
Но мы знаем, что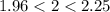 
- это очевидно. Тогда извлечём корень, и в силу его монотонного возрастания, знаки не поменяются. Тогда
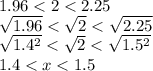
Отлично, мы определили х до первого знака после запятой. Определим его и до второй.
Есть такое число, 1.9881 = 1.41² и 2.0164 = 1.42²
Очевидно, что вот так:
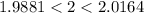
Тогда опять же из-за прекрасной функции корня получаем красивую вещь:
То есть, так как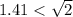 
, то 
, наибольший порядок у у равен порядку 1.41 - а это -2. Тогда у не будет влиять на второй знак после запятой в числе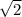 
, тогда 1.41 - десятичная запись 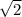до второго знака.
