в 5а - 36
в 5б - 44
Пошаговое объяснение:
1) так как людей не может быть дробное колличество, то количество учеников 5а класса должно делиться на 9, а 5б на 11
2) будем искать методом подбора:
на 11 делятся только числа: 11, 22, 33, 44, 55, 66, 77(далее уже больше общего количества учеников, что невозможно)
80 - 11 = 69 не делиться нацело на 9, значит не подходит
80- 22=58 не подходит по той же причине
80 - 33 = 47 не подходит по той же причине
80- 44=36 , 36 делится на 9, значит подходит
(далее можешь по такому же принципу проверить все остальные числа делящиеся на 11, но подходящего ответа больше не будет)
итак в 5а - 36 человек
в 5б - 44 человека
1. 
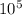= 100000
2. 899910
Пошаговое объяснение:
1. Как известно, не бывает шестизначных номеров, начинающихся с нуля, поэтому надо подсчитать их количество и вычесть его из общего числа комбинаций. Число номеров, первая цифра у которых 0, найдем по формуле размещений с повторениями, «зафиксировав» ноль т.е. на каждом из пяти остальных возможных мест может встретиться любая из десяти цифр от
0 до 9.
Тогда число таких комбинаций:
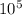= 100000
2. Первую букву можно выбрать , вторую при этом столькими же , тогда по правилу умножения можно составить буквенную часть номера.
Номера 0000 нет, всего можно составить 10*10*10*10-1=9999 числовых номеров.
90*9999=899910 разных номеров можно составить указанным
3. Количество вариантов выбора двух молодых людей из 10:
C(10,2) = 10! / ( 2! · (10 - 2!) = 9 · 10 / 2 = 45.
Количество вариантов выбора двух девушек из 13:
C(13,2) = 13! / ( 2! · (13 - 2!) = 12 · 13 / 2 = 78.
Общее число исходов при выборе однополых пар.
Сложим количество исходов для девушек и количество исходов для молодых людей.
N = C(10,2) + C(13,2) = 45 + 78 = 123.
ответ: Существует 123 исхода.
2•8=16