2)(5,69 - 2,85) * 1,5 + 7,8 * 5,4 - 23,88=22,5
1. 5,69 - 2,85=2,84
2. 2,84*1,5=4,26
3. 7,8*5,4=42,12
4. 4,26+42,12=46,38
5. 46,38-23,88=22,5
3) (98,6 * 0,1 + 14 * 0,15)* 3,5 - 36,86=5
1. 98,6 * 0,1=9,86
2. 14 * 0,15=2,1
3. 9,86+2,1=11,96
4. 11,96*3,5=41,86
5. 41,86-36,86=6
4)(103,92 - 5,6 * 4,2)* 0,75 - 2,8 * (10 - 8,25)=55,4
1. 5,6 * 4,2=23,52
2. 103,92-23,52=80,4
3. 10-8,25=1,75
4. 80,4*0,75=60,3
5. 2,8*1,75=4,9
6. 60,3-4,9=55,4
Пошаговое объяснение:
Общую схему рассмотрим в примере 1) 2,1(6).
Пусть число а,b(c) периодичное, где а - целая часть, b - число в предпериоде, c - число в периоде, в нашем примере а=2, b=1, c=6. Чтобы преобразовать эту дробь в обыкновенную нужно придерживаться следующему правилу:
а) Считаем количество цифр в периоде десятичной дроби и обозначаем количество цифр через k, в нашем примере k=1, так как число 6 состоит из одной цифры;
б) Считаем количество цифр, стоящих в предпериоде, то есть количество цифр, стоящих после запятой, но до периода десятичной дроби и обозначаем количество цифр через m, в нашем примере m=1, так как число 1 состоит из одной цифры;
в) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа , в нашем примере n=16;
г) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа , в нашем примере s=1;
д) Подставляем найденные значения в формулу
Нетрудно видеть, что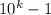 
состоит из k цифр 9, а 
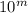из m цифр 0 после 1.
В нашем примере
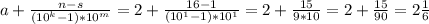
2) 5,14(33) ⇒ a=5, k=2, m=2, n=1433, s=14. Тогда
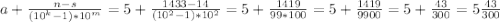
3) 0,11(35) ⇒ a=0, k=2, m=2, n=1135, s=11. Тогда
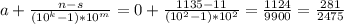
4) 0,214(45) ⇒ a=0, k=2, m=3, n=21445, s=214. Тогда
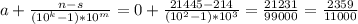
t²-6t+5=0
t=5
t=1
x²+1=5
x²+1=1
x1=-2
x2=0
x3=2