Пошаговое объяснение:
1) с первым интегралом все достаточно просто
здесь мы перейдем к повторным интегралам и получим вот что
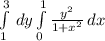
сначала вычисляем внутренний интеграл
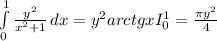
теперь вычисляем внешний интеграл
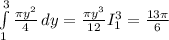
это и есть ответ 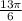
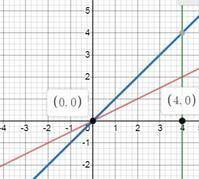
2) со вторым придется построить графики, чтобы определить границы интегрирования по х
тут мы видим, что х изменяется 0≤х≤4
в общем-то нижний предел интегрирования можно было бы найти и путем выяснения, в какой точке пересекаются графики (через уравнение х/2 = х корень данного уравнения х=0), но лучше все же строить график
теперь, собственно приступаем к переходу и интеграции
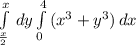
внутренний интеграл
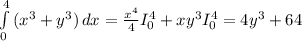
внешний интеграл
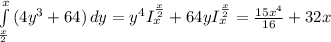
ответ