Пусть х км в час - скорость первого, который шел из А в В.
y км в час - скорость второго, который шел из В в А.
За 5 часов первый х км, второй - 5y км, вместе они км.
Первое уравнение:
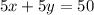
После встречи первый шел путь, проийденный вторым до встречи,
т. е 5y км со скоростью (х-1) км в час,
второй - 5х км со скоростью у км в час
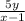час - время первого после встречи
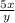час - время второго после встречи
По условию первый прибув до пункту В на 2 години раніше, ніж другий - до пункту А.
Второе уравнение:
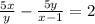
Решаем систему двух уравнений: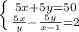 
подстановки:
⇒ 
⇒ 
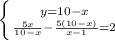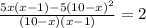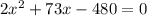
D=73²+4·2·480=5329+3840=9169
√D≈
Проверяйте условие задачи
пусть х-скорость первого автомобиля, а у-скорость второго автомобиля Составим систему из двух уравнений. Первое уравнение 360/у-360/х=0,5 и второе 3х-3у=30 Второе сократим на 3, тогда получим х-у=10. выразим из этого уравнения х=у+10 и подставим в первое уравнение. Получим 360/у-360/(у+10)-0,5=0 Получим 720(у+10)-720у-(у+10)у=0
У^2+10y-7200=0 Найдем через дискриминант корни уравнения D=100+28800=28900=170^2
y₁=80 y₂=-90 (посторонний корень, так как скорость не может быть отрицательной) Следовательно у=80, а х=80+10=90
ответ: скорость первого автомобиля 90 км/ч, а второго 80 км/ч
Пошаговое объяснение
получи решение
3х кг - за первый день.
х+54 кг - за второй день.
3х+х+(х+54)= 161 (кг) - за три дня, по условию задачи.
Тогда
3х+х+х+54=161
5х=161-54
5х=107
х=107/5
х=21,4 (кг) - за второй день.
21,4*3=64,2 (кг) - за первый день.
21,4+54=75,4 (кг) - за второй день.
Проверка
64,2+21,4+75,4=161(кг) - за три дня, по условию задачи.
ответ: 64,2кг; 21,4кг; 75,4кг.