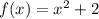 определена на множестве E
определена на множестве E 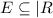
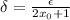 где
где 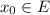 .
. на области
на области 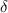 от
от  (то есть:
(то есть: 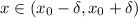 ) выполняется
) выполняется 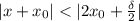 .
.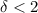 , выполняется
, выполняется 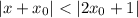 .
.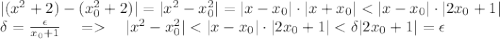
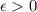 есть
есть 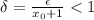 , на области которой выполняется
, на области которой выполняется 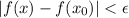
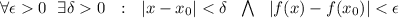 ). Следовательно -
). Следовательно - 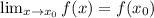 .
.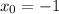 нужно отдельно доказать предел
нужно отдельно доказать предел 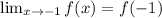 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 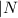 тоже подмножество
тоже подмножество  , значит
, значит 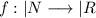 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 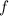 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 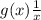 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 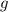 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 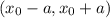 "...
"...а)
делится на 5, если последняя цифра 0 или 5
сумма цифр 11
... 0 0 - последняя цифра 0 не может быть, так как первое число не может быть двухзначным
0 5 - чтобы сумма цифр была 11, первая цифра должна быть 6
( 11 - 5 = 6)
ОТВЕТ: 605
б)
3 = 1 + 2 = 2 + 1
если последняя цифра 1, то 1 цифра должна быть 2, но так не получится, значит цифра десятков должна быть с переходом через разряд - это 5.
5 1
видим, что в разряде сотен цифра 2 ( 2 + 1 = 3... нам по условию нужно получить сумму равную 403)
251 + 152 = 403 - верно
ОТВЕТ: 251 и 152
Пол года это 6 месяцев.
300/6 = 50 рублей чистого роста в месяц
500 - 100%
550 - х%
х = (550х100)/500 = 110%
110% - 100% = 10%
ответ: Прирост вклада составляет 10% в месяц.