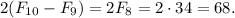А. Здесь подходит формула перестановок
Pn=n*(n−1)*(n−2)*...=n!,
поскольку шифры отличаются между собой только порядком расположения элементов (цифр), но не самими элементами. В условии написано, что шифр состоит из различных цифр (нет повторений, учитывается порядок), поэтому размещения и сочетания не подходят. Будем переставлять их всеми возможными (число элементов остается неизменными, меняется только их порядок).
Первую цифру шифра можно выбрать из 4, вторую - из 3 оставшихся цифр, третью - из 2 оставшихся, четвёртую - из 1 оставшейся. Таким образом, возможное количество вариантов:
Р(4)=4!=1*2*3*4=24 (варианта)
Б. Первую цифру шифра можно выбрать из 5, вторую - из 4 оставшихся, третью - из 3 оставшихся, четвёртую - из 2 оставшихся. поэтому все возможные варианты шифра - это:
P(5)=5!=5*4*3*2=120 (вариантов)
В. Первую цифру шифра можно выбрать из 6, вторую - из 5 оставшихся, третью - из 4 оставшихся, четвёртую - из 3 оставшихся. Здесь подойдет формула размещения, потому что порядок имеет значение, но не все цифры могут состоять в шифре (дано шесть цифр, а шифр должен состоять из 4). Тогда возможное количество вариантов составляет:
(вариантов)
ответ: 24, 120, 360.
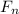- количество произносимых слов длины n, начинающихся с 1. Очевидно, количество произносимых слов, начинающихся с 0 также равно 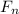(одни получаются из других взаимной заменой 0 и 1). Тогда, если n≥3, то любое произносимое слово длины n, начинающееся с 1, можно получить одним из следующих двух 
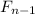штук, причем, полученные слова обязательно будут произносимыми, т.к. начинаются на "10" и не могут содержать три нуля или три единицы подряд. 
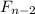штук. Это слово также произносимо, т.к. начинается на 110, и, значит, не содержит трех нулей или единиц подряд.
и легко видеть, что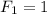 
( есть только одно произносимое слово "1" длины 1, начинающееся на "1") и 
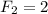(есть только два произносимых слова "10" и "11" длины 2, начинающиеся с "1"). Таким образом, количество всех произносимых слов длины n равно равно 
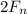и равно удвоенному n-ому числу Фибоначчи. Т.е., начиная с 
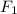, последовательность 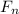имеет вид 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ..., где каждое следующее число - сумма двух предыдущих.
, 
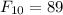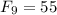, а значит, искомая разность равна
