1) 89/7 = 12 5/7 (89:7=12: остаток 5)
318/15 = 21 3/15 = 21 1/5 (318:15=21; остаток 3)
2) 4×16+5=69 => 69/16
101×5+4=509 => 509/5
3) 1 7/15–24/25 = 110/75–72/75 = 38/75
7/8 + 1 3/8 = 1 10/8 = 2 2/8 = 2 1/4
6 3/4 × 1 7/9 = 27/4 × 16/9 = 3×4 = 12
3 1/5 ÷ 2 2/5 = 16/5 ÷ 12/5 = 16/5 × 5/12 = 16/12 = 4/3 = 1 1/3
4) Пусть брат Алёши сделал х журавликов. Тогда сам Алёша сделал 5х журавликов. Так как вместе они сделали 60 журавликов, составлю уравнение:
х+5х=60
6х=60
х=10(ж.) – сделал брат Алеши;
10×5=50(ж.) – сделал Алеша.
ответ: брат Алеши сделал 10 журавликов, а сам Алеша сделал 50 журавликов.
5) VII/X = 7/10
Переставим палочку из числителя в знаменатель. Будет выглядеть так:
VI/IX
IX – это число 9. VI – число 6.
6/9 и будет 2/3, если сократить эту дробь на 3 :)
Большая сторона первоначального прямоугольника x.
Есть два возможный варианта: 1) прямоугольник разрезали по меньшей стороне; 2) прямоугольник разрезали по большей стороне. Рассмотрим их оба:
1) пусть одна сторона первого прямоугольника y, тогда вторая 6-y. Вторые стороны у обоих x.
Площади: xy кв.ед. у первого, x·(6-y) кв.ед. у второго. У первого в 3 раза больше:
xy = 3x·(6-y)
Периметры: (x+y)·2 у первого, (x+6-y)·2 у второго. У первого в 2 раза больше:
(x+y)·2 = 2·(x+6-y)·2
Составим и решим систему уравнений:

Большая сторона первоначального прямоугольника 1,5.
2) пусть одна сторона первого прямоугольника y, тогда вторая x-y. Вторые стороны у обоих 6.
Площади: 6y кв.ед. у первого, 6(x-y) кв.ед. у второго. У первого в 3 раза больше:
6y = 3·6(x-y)
Периметры: у первого (y+6)·2, у второго (x-y+6)·2, у первого в 2 раза больше:
(y+6)·2 = 2·(x-y+6)·2.
Составим и решим систему уравнений:
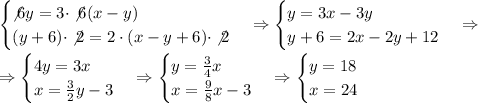
Большая сторона первоначального прямоугольника 24.
ответ: 1,5 или 24.
200 = 2 * 2 * 2 * 5 * 5
27 и 200 - взаимно простые числа, так как у них нет общих делителей, кроме единицы.
27/200 = 135/1000 - доп.множ. 5
ответ: 27/200 - несократимая дробь, которую можно представить в виде десятичной дроби (27/200 = 0,135).